Modélisation statistique

03. Modèles linéaires

Léo Belzile, HEC Montréal

2024

Quels sont les éléments d’un modèle

Un modèle stochastique (ou aléatoire) combine typiquement

• une loi pour les données avec
• une formule liant les paramètres ou la moyenne conditionnelle d’une variable réponse \(Y\) à des variables explicatives \(\mathbf{X}\)

Les modèles sont des “golems” qui servent à obtenir des réponses à nos questions.

Objectifs de la modélisation

1. Évaluer les effets des variables explicatives sur la moyenne d’une variable réponse.
2. Tester les effets de manipulations expérimentales ou d’autres variables explicatives sur une réponse.
3. Prédire la réponse pour de nouvelles combinaisons de variables explicatives.

Modèle linéaire

Un modèle linéaire est un modèle qui décrit la moyenne d’une variable réponse continue \(Y_i\) d’un échantillon aléatoire de taille \(n\) comme fonction linéaire des variables explicatives (également appelés prédicteurs, régresseurs ou covariables) \(X_1, \ldots, X_p\), \[\begin{align} \underset{\text{moyenne conditionnelle}}{\mathsf{E}(Y_i \mid \boldsymbol{X}_i=\boldsymbol{x}_i)}=\mu_i=\underset{\substack{\text{combinaison linéaire (somme pondérée)}\\ \text{de variables explicatives}}}{\beta_0 + \beta_1x_{i1} + \cdots + \beta_p x_{ip}}\equiv \mathbf{x}_i\boldsymbol{\beta}. \end{align}\] où

• \(\mathbf{x}_i = (1, x_{i1}, \ldots, x_{ip})\) est un vecteur ligne de taille \((p+1)\) contenant les variables explicatives de l’observation \(i\)
• \(\boldsymbol{\beta} = (\beta_0, \ldots, \beta_p)^\top\) est un vecteur colonne de longueur \(p+1\) contenant les coefficients de la moyenne.

Formulation alternative

Pour l’observation \(i\), on peut écrire \[\begin{align*} \underset{\text{observation}\vphantom{\mu_i}}{Y_i} = \underset{\text{moyenne } \mu_i}{\vphantom{Y_i}\mathbf{x}_i\boldsymbol{\beta}} + \underset{\text{aléa}\vphantom{\mu_i}}{\vphantom{Y_i}\varepsilon_i}, \end{align*}\] où \(\varepsilon_i\) sont des aléas indépendents additifs satisfaisant:

• \(\mathsf{E}(\varepsilon_i \mid \mathbf{x}_i) = 0\); on fixe l’espérance de l’aléa à zéro car on postule qu’il n’y a pas d’erreur systématique.
• \(\mathsf{Var}(\varepsilon_i \mid \mathbf{x}_i) = \sigma^2\); la variance \(\sigma^2\) sert à tenir compte du fait qu’aucune relation linéaire exacte ne lie \(\mathbf{x}_i\) et \(Y_i\), ou que les mesures de \(Y_i\) sont variables.

Le modèle linéaire normal \[Y_i \mid \boldsymbol{X}_i=\boldsymbol{x}_i \sim \mathsf{normale}(\mathbf{x}_i\boldsymbol{\beta}, \sigma^2).\]

Commentaires sur la formulation

• la moyenne est conditionnelle aux valeurs de \(\mathbf{X}\) implique simplement que l’on considère les variables explicatives comme connues à l’avance, ou que \(X_1, \ldots, X_p\) sont fixes (non-aléatoires).
• Les coefficients \(\boldsymbol{\beta}\) sont les mêmes pour toutes les observations, mais le vecteurs de variables explicatives \(\mathbf{x}_i\) peut différer d’une observation à l’autre.
• Le modèle est linéaire en \(\beta_0, \ldots, \beta_p\), pas nécessairement dans les variables explicatives.
  • la spécification \(\mathsf{E}(Y \mid X =x) = \beta_0 + \beta_1 x^\beta_2\) est nonlinéaire
  • tandis que \(\mathsf{E}(Y \mid X =x) = \beta_0 + \beta_1 x + \beta_2 x^2\) est un modèle linéaire
  • tout comme \(\mathsf{E}(Y \mid X =x) = \beta_0 + \sum_{j=1}^p\beta_j \mathbf{1}_{x \in (a_j, a_{j+1}]}\) où \(a_1 < \cdots < a_{p+1}\), avec \(\mathbf{1}_{\cdot}\) une variable indicatrice binaire qui vaut un si l’énoncé est vrai et zéro sinon.

Illustration de modèle linéaires complexes

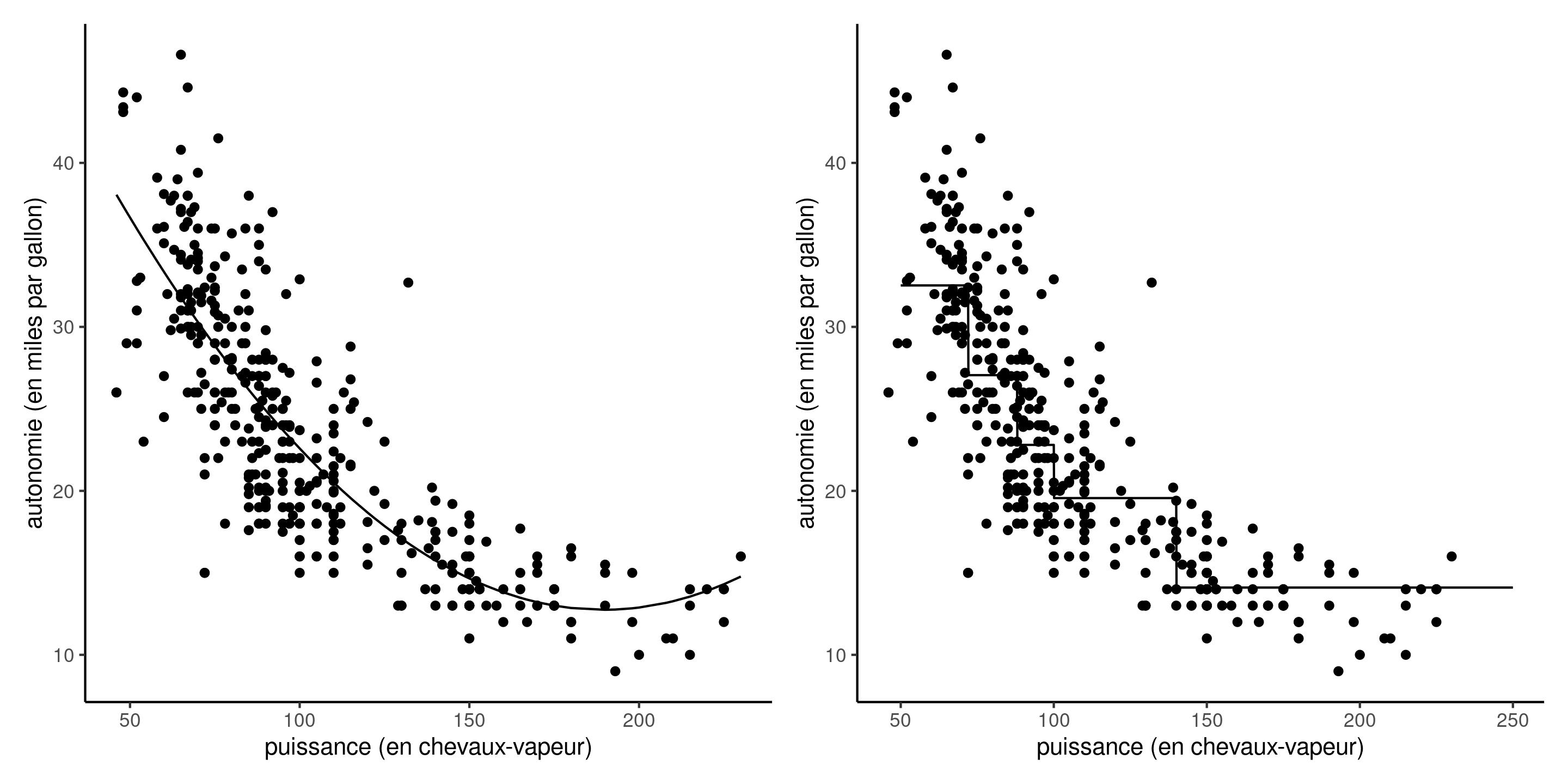
Figure 1: Régression linéaire avec terme quadratique (gauche) et modèle avec fonction de moyenne affine par morceaux pour chaque quintile (droite), pour l’autonomie d’essence de véhicules en fonction de la puissance de leur moteur.

On peut toujours transformer une variable continue en variable catégorielle pour un modèle pour \(Y\) en fonction de \(X\), mais au prix de coefficients supplémentaires.

Notation

Pour simplifier la notation, nous agrégeons les observations en utilisant la notation vectorielle et matricielle suivante: \[\begin{align*} \boldsymbol{Y} = \begin{pmatrix} Y_1 \\ Y_2 \\ \vdots \\ Y_n \end{pmatrix}, \; % \boldsymbol{\varepsilon} = %\begin{pmatrix} % \varepsilon_1 \\ % \varepsilon_2 \\ % \vdots \\ % \varepsilon_n % \end{pmatrix}, \; \mathbf{X} = \begin{pmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1p} \\ 1 & x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & x_{n2} & \cdots & x_{np} \end{pmatrix} , \; \boldsymbol{\beta} = \begin{pmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \\ \vdots \\ \beta_p \end{pmatrix} \end{align*}\] On désigne par \(\mathbf{X}\) la matrice du modèle \(n \times (p+1)\) constituée d’une colonne de uns, concaténée aux \(p\) vecteurs colonnes de variables explicatives.

La \(i\)e ligne de \(\mathbf{X}\) est dénotée \(\mathbf{x}_i\).

Exemple 1 — cohérence de description de produits

L’étude 1 de Lee et Choi (2019) (base de données LC19_S1, paquet hecedsm) considère l’impact sur la perception d’un produit de la divergence entre la description textuelle et l’image.

Dans leur première expérience, un paquet de six brosses à dents est vendu, mais l’image montre soit un paquet de six, soit une seule).

Les auteurs ont également mesuré la familiarité préalable avec la marque de l’article. Les participants ont été recrutés à l’aide d’un panel en ligne.

Variables:

• prodeval: score moyen d’évaluation du produit sur trois échelles de 9 points (les valeurs les plus élevées sont les meilleures)
• familiarity: échelle de Likert de 1 à 7 pour la familiarité avec la marque
• consistency: groupes d’images et de textes, soit « cohérents », soit « incohérents ».

Exemple 2 – apprendre à lire

La base de données BSJ92 du paquet hecedsm contient les résultats d’une expérience de Baumann, Seifert-Kessell, et Jones (1992) sur l’efficacité de différentes stratégies de lecture sur la compréhension d’enfants.

Soixante-six élèves de quatrième année ont été assignés au hasard à l’un des trois groupes expérimentaux suivants : (a) un groupe « Think-Aloud » (TA), dans lequel les élèves ont appris diverses stratégies de contrôle de la compréhension pour la lecture d’histoires (par exemple : auto-questionnement, prédiction, relecture) par le biais de la réflexion à haute voix; (b) un groupe lecture dirigée-activité de réflexion (DRTA), dans lequel les élèves ont appris une stratégie de prédiction-vérification pour lire et répondre aux histoires; ou (c) un groupe activité de lecture dirigée (DRA), un groupe contrôle dans lequel les élèves se sont engagés dans une lecture guidée non interactive d’histoires.

Variables:

• group: facteur pour le groupe expérimental, soit DRTA, TA et DR.
• pretest1: score (sur 16) sur le test pré-expérience pour la tâche de détection des erreurs
• posttest1: score (sur 16) sur le test post-expérience pour la tâche de détection des erreurs

Exemple 3 — Salaire dans un collège

On s’intéresse à la discrimination salariale dans un collège américain, au sein duquel une étude a été réalisée pour investiguer s’il existait des inégalités salariales entre hommes et femmes. Les données observationnelles college du paquet hecmodstat incluent les variables suivantes

• salaire: salaire de professeurs pendant l’année académique 2008–2009 (en dollars USD).
• echelon: échelon académique, soit adjoint (adjoint), aggrégé (aggrege) ou titulaire (titulaire).
• domaine: variable catégorielle indiquant le champ d’expertise du professeur, soit appliqué (applique) ou théorique (theorique).
• sexe: indicateur binaire pour le sexe, homme ou femme.
• service: nombre d’années de service.
• annees: nombre d’années depuis l’obtention du doctorat.

Exemple 4 — suggestion de montants de dons

L’étude 1 de Moon et VanEpps (2023) (données MV23_S1, paquet hecedsm) porte sur la proportion de donateurs à un organisme de charité. Les participants au panel en ligne avaient la possibilité de gagner 25$ et de faire don d’une partie de cette somme à l’organisme de leur choix. Les données fournies incluent uniquement les personnes qui n’ont pas dépassé ce montant et qui ont indiqué avoir fait un don d’un montant non nul.

Variables:

• before: est-ce que la personne a déjà donné à l’organisme de charité (0 pour non, 1 pour oui)
• condition: facteur pour le groupe expérimental, soit open-ended pour un montant libre ou quantity pour le groupe avec montants suggérés
• amount: montant du don, NA si la personne n’a rien donné.

Analyse exploratoire des données

L’analyse exploratoire des données est une procédure itérative par laquelle nous interrogeons les données, en utilisant des informations auxiliaires, des statistiques descriptives et des graphiques, afin de mieux informer notre modélisation.

Elle est utile pour mieux comprendre

• les caractéristiques des données (plan d’échantillonnage, valeurs manquantes, valeurs aberrantes)
• la nature des observations, qu’il s’agisse de variables réponse ou explicatives
• la relation entre les variables.

Voir le Chapitre 11 de Alexander (2023) pour des exemples.

Liste de vérifications pour l’analyse exploratoire

Vérifier

• que les variables catégorielles sont adéquatement traitées comme des facteurs (factor).
• que les valeurs manquantes sont adéquatement déclarées comme telles (code d’erreur, 999, etc.)
• s’il ne vaudrait mieux pas retirer certaines variables explicatives avec beaucoup de valeurs manquantes.
• s’il ne vaudrait mieux pas fusionner des modalités de variables catégorielles si le nombre d’observation par modalité est trop faible.
• qu’il n’y a pas de variable explicative dérivée de la variable réponse
• que le sous-ensemble des observations employé pour l’analyse statistique est adéquat.
• qu’il n’y a pas d’anomalies ou de valeurs aberrantes (par ex., 999 pour valeurs manquantes) qui viendraient fausser les résultats.

Analyse exploratoire pour l’exemple 1

Considérons un modèle linéaire pour la note moyenne d’évaluation du produit, prodeval, en fonction de la familiarité de la marque et du facteur expérimental consistency.

data(LC19_S1, package = "hecedsm")
str(LC19_S1)
## tibble [96 × 5] (S3: tbl_df/tbl/data.frame)
##  $ prodeval   : num [1:96] 9 8.33 8.67 7.33 9 ...
##  $ familiarity: int [1:96] 7 7 7 7 6 5 7 7 4 7 ...
##  $ consistency: Factor w/ 2 levels "consistent","inconsistent": 1 1 1 1 1 1 1 1 1 1 ...
##  $ gender     : Factor w/ 2 levels "male","female": 1 2 1 2 1 1 2 1 1 1 ...
##  $ age        : int [1:96] 22 26 35 26 39 34 30 33 24 42 ...
length(unique(LC19_S1$prodeval))
## [1] 19

La variable réponse prodeval est fortement discrétisée, avec seulement 19 valeurs uniques comprises entre 2.33 et 9.

Matrice du modèle pour l’exemple 1

La variable consistency vaut 0 si la description du texte est cohérente avec l’image, et 1 si elle est incohérente.

modmat <- model.matrix(
     ~ familiarity + consistency,
     data = LC19_S1)
tail(modmat, n = 5L) # cinq dernières lignes
##    (Intercept) familiarity consistencyinconsistent
## 92           1           6                       1
## 93           1           4                       1
## 94           1           7                       1
## 95           1           7                       1
## 96           1           7                       1
dim(modmat) # dimension de la matrice du modèle
## [1] 96  3

Analyse exploratoire de l’exemple 3

Le salaire augmente avec les années de service, mais il y a une plus grande hétérogénéité dans le salaire des professeurs titulaires.

Figure 2: Répartition des salaires en fonction de l’échelon et du nombre d’années de service

Les professeurs adjoints qui ne sont pas promus sont généralement mis à la porte, aussi il y a moins d’occasions pour que les salaires varient sur cette échelle.

Les variables annees et service sont fortement corrélées, avec une corrélation linéaire de 0.91.

Analyse exploratoire pour l’exemple 3

Il y a peu de femmes dans l’échantillon. Si on fait un tableau de contingence de l’échelon et du sexe, on peut calculer la proportion relative homme/femme dans chaque échelon: 16% des profs adjoints, 16% pour les aggrégés, mais seulement 7% des titulaires alors que ces derniers sont mieux payés en moyenne.

Tableau de contingence donnant le nombre de professeurs du collège par sexe et par échelon académique.

	adjoint	aggrege	titulaire
femme	11	10	18
homme	56	54	248

Analyse exploratoire pour l’exemple 4

data(MV23_S1, package = "hecedsm")
str(MV23_S1)
## tibble [869 × 4] (S3: tbl_df/tbl/data.frame)
##  $ before   : int [1:869] 0 1 0 1 1 1 1 0 1 0 ...
##  $ donate   : int [1:869] 0 0 0 1 1 0 1 0 0 1 ...
##  $ condition: Factor w/ 2 levels "open-ended","quantity": 1 1 1 1 2 2 2 1 1 1 ...
##  $ amount   : num [1:869] NA NA NA 10 5 NA 20 NA NA 25 ...
summary(MV23_S1)
##      before          donate          condition       amount    
##  Min.   :0.000   Min.   :0.00   open-ended:407   Min.   : 0.2  
##  1st Qu.:0.000   1st Qu.:0.00   quantity  :462   1st Qu.: 5.0  
##  Median :1.000   Median :1.00                    Median :10.0  
##  Mean   :0.596   Mean   :0.73                    Mean   :10.7  
##  3rd Qu.:1.000   3rd Qu.:1.00                    3rd Qu.:15.0  
##  Max.   :1.000   Max.   :1.00                    Max.   :25.0  
##  NA's   :1                                       NA's   :235

Si nous incluons amount comme variable réponse, les 235 observations manquantes seront supprimées.

• Cela ne pose pas de problème si nous voulons comparer le montant moyen des personnes qui ont fait un don
• Dans le cas contraire, nous devons transformer les NA en zéros.

Les variables binaires donate et before sont toutes deux des facteurs encodés comme 0/1.

Quelles variables explicatives inclure?

Avec des données expérimentales, seules les variables manipulées expérimentalement (affectation aléatoire aux groupes) sont nécessaires.

• Des covariables antécédantes ou concomitantes sont ajoutées si elles sont corrélées avec la réponse pour augmenter la puissance (par exemple, le résultat du pré-test pour Baumann, Seifert-Kessell, et Jones (1992), qui donne une mesure de la capacité individuelle de l’élève).

Pour les données observationnelles, nous avons besoin d’un modèle pour prendre en compte les facteurs de confusion potentiels.

Interprétation des coefficients — ordonnée à l’origine

La spécification de la moyenne est \[\begin{align*} \mathsf{E}(Y_i \mid \boldsymbol{X}_i = \boldsymbol{x}_i) = \beta_0 + \beta_1 x_{i1} + \ldots + \beta_p x_{ip}. \end{align*}\] L’ordonnée à l’origine \(\beta_0\) est la valeur moyenne de \(Y\) lorsque toutes les variables explicatives du modèles sont nulles, soit \(\boldsymbol{x}_i=\boldsymbol{0}_p\). \[\begin{align*} \beta_0 &= \mathsf{E}(Y \mid X_1=0,X_2=0,\ldots,X_p=0) \\ &= \beta_0 + \beta_1 \times 0 + \beta_2 \times 0 + \cdots + \beta_p \times 0 \end{align*}\] Bien sur, il se peut que cette interprétation n’ait aucun sens dans le contexte étudié. Centrer les variables explicatives numériques (pour que leurs moyennes soit zéro) permet de rendre l’ordonnée à l’origine plus interprétable.

Interprétation des coefficients

En régression linéaire, le paramètre \(\beta_j\) mesure l’effet de la variable \(X_j\) sur la variable \(Y\) une fois que l’on tient compte des effets des autres variables explicatives.

• pour chaque augmentation d’une unité de \(X_j\), la réponse \(Y\) augmente en moyenne de \(\beta_j\) lorsque les autres variables demeurent inchangées.

\[\begin{align*} \beta_1 &= \mathsf{E}(Y \mid X_1=x_1+1,X_2=x_2, \ldots, X_p=x_p) \\ & \qquad \qquad - \mathsf{E}(Y \mid X_1=x_1,X_2=x_2,\ldots,X_p=x_p) \\ &= \left\{\beta_1 (x_1+1) + \beta_2 x_2 + \cdots \beta_p x_p \right\} \\ & \qquad \qquad -\left\{\beta_1 x_1 + \beta_2 x_2 + \cdots \beta_p x_p \right\} \end{align*}\]

Effet marginal

On définit l’effet marginal comme la dérivée première de la moyenne conditionnelle par rapport à \(X_j\), soit \[\text{effet marginal de }X_j = \frac{\partial \mathsf{E}(Y \mid \boldsymbol{X})}{ \partial X_j}.\]

Le coefficient \(\beta_j\) est aussi l’effet marginal de la variable \(X_j\).

Modèle linéaire avec une seule variable indicatrice

Considérons par exemple un modèle linéaire pour les données de Moon et VanEpps (2023) qui inclut le montant (amount) (en dollars, de 0 pour les personnes qui n’ont pas fait de don, jusqu’à 25 dollars).

L’équation du modèle linéaire simple qui inclut la variable binaire condition est \[\begin{align*} \mathsf{E}(\texttt{amount} \mid \texttt{condition})&= \beta_0 + \beta_1 \mathbf{1}_{\texttt{condition}=\texttt{quantity}}. \\&= \begin{cases} \beta_0, & \texttt{condition}=0, \\ \beta_0 + \beta_1 & \texttt{condition}=1. \end{cases} \end{align*}\]

• L’ordonnée à l’origine \(\beta_0\) est la moyenne du groupe contrôle (open-ended).
• La moyenne du groupe traitement (quantity) est \(\beta_0 + \beta_1 = \mu_1\) et
• \(\beta_1=\mu_1-\mu_0\) est la différence du montant moyen de dons entre le groupe open-ended et le groupe quantity.

Régression linéaire simple avec variable indicatrice

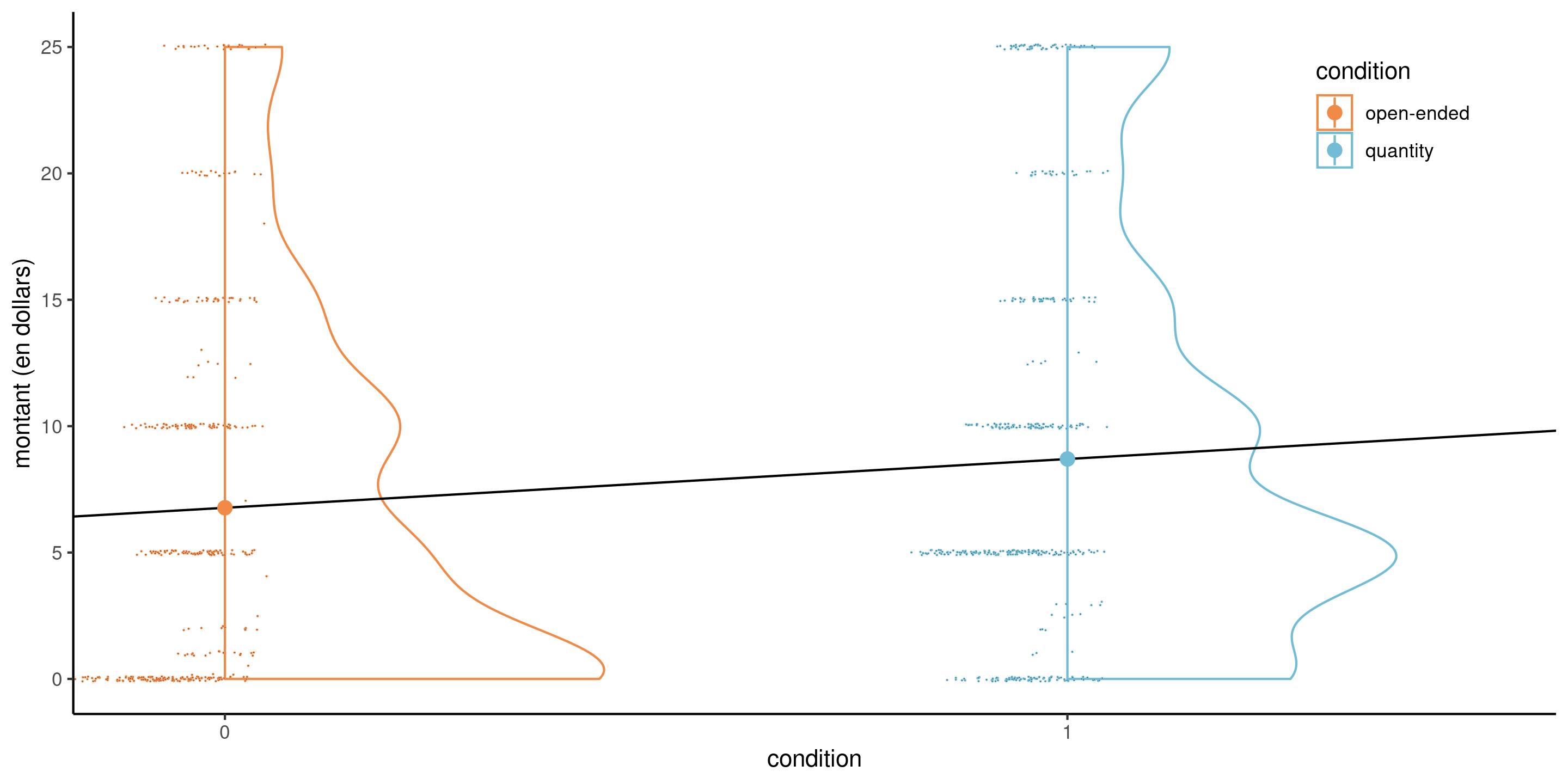
Figure 3: Modèle linéaire simple pour les données MV23_S1 avec condition comme variable explicative binaire, avec nuage de points décalés et un diagramme en demi-violin. Les cercles indiquent les moyennes de l’échantillon.

Même si le modèle linéaire définit une droite, cette dernière ne peut être évaluée qu’à \(0\) ou \(1\)

Les données sont fortement discrétisées, avec beaucoup de doublons et de zéros, mais la taille de l’échantillon \((n=869)\) est conséquente.

Codage binaire pour les variables catégorielles

Considérons l’étude de Baumann, Seifert-Kessell, et Jones (1992) et la seule variable group. Les données sont classées par groupe : les 22 premières observations concernent le groupe DR, les 22 suivantes le groupe DRTA et les 22 dernières le groupe TA.

data(BSJ92, package = "hecedsm")
class(BSJ92$group) # Vérifier que group est un facteur
## [1] "factor"
levels(BSJ92$group) # première valeur est la catégorie de référence
## [1] "DR"   "DRTA" "TA"
# Imprimer trois lignes de la matrice du modèle
# (trois enfants de groupes différents)
model.matrix(~ group, data = BSJ92)[c(1,23,47),]
##    (Intercept) groupDRTA groupTA
## 1            1         0       0
## 23           1         1       0
## 47           1         0       1
# Comparer avec les niveaux des facteurs
BSJ92$group[c(1,23,47)]
## [1] DR   DRTA TA  
## Levels: DR DRTA TA

Analyse de variance

Si nous ajustons un modèle avec groupe comme variable catégorielle, la spécification de la moyenne du modèle est \[\mathsf{E}(Y \mid \texttt{group})= \beta_0 + \beta_1\mathbf{1}_{\texttt{group}=\texttt{DRTA}} + \beta_2\mathbf{1}_{\texttt{group}=\texttt{TA}}.\] Puisque la variable group est catégorielle avec \(K=3\) niveaux, il nous faut mettre \(K-1 = 2\) variables indicatrices.

Avec la paramétrisation en termes de traitements (option par défaut), on obtient

• \(\mathbf{1}_{\texttt{group}=\texttt{DRTA}}=1\) si group=DRTA et zéro sinon,
• \(\mathbf{1}_{\texttt{group}=\texttt{TA}}=1\) si group=TA et zéro sinon.

Étant donné que le modèle comprend une ordonnée à l’origine et que le modèle décrit en fin de compte trois moyennes de groupe, nous n’avons besoin que de deux variables supplémentaires.

Variables catégorielles

Avec la paramétrisation en termes de traitements, la moyenne du groupe de référence est l’ordonnée à l’origine, \(\mu_{\texttt{DR}}=\beta_0\).

Table 1: Paramétrisation des variables indicatrices pour le modèle en termes de traitements.

	(Intercept)	groupDRTA	groupTA
DR	1	0	0
DRTA	1	1	0
TA	1	0	1

Interprétation des paramètres

Si group=DR (référence), les deux variables indicatrices binaires groupDRTA et groupTA sont nulles. La moyenne de chaque groupe est

• \(\mu_{\texttt{DR}} = \beta_0\),
• \(\mu_{\texttt{DRTA}}=\beta_0 + \beta_1\) et
• \(\mu_{\texttt{TA}} = \beta_0 + \beta_2\).

Ainsi, \(\beta_1\) est la différence de moyenne entre les groupes DRTA etDR, et de la même façon \(\beta_2=\mu_{\texttt{TA}}- \mu_{\texttt{DR}}\).

Modèle linéaire pour données du collège

On considère un modèle de régression pour les données college qui inclut le sexe, l’échelon académique, le nombre d’années de service et le domaine d’expertise (appliquée ou théorique).

Le modèle linéaire postulé s’écrit

\[\begin{align*} \texttt{salaire} &= \beta_0 + \beta_1 \mathbf{1}_{\texttt{sexe}=\texttt{femme}} +\beta_2 \mathbf{1}_{\texttt{domaine}=\texttt{theorique}} \\&\quad +\beta_3 \mathbf{1}_{\texttt{echelon}=\texttt{aggrege}} +\beta_4 \mathbf{1}_{\texttt{echelon}=\texttt{titulaire}} +\beta_5 \texttt{service} + \varepsilon. \end{align*}\]

Table 2: Estimations des coefficients du modèle linéaire pour les données \(\texttt{college}\) (en dollars USD, arrondis à l’unité).

\(\widehat{\beta}_0\)	\(\widehat{\beta}_1\)	\(\widehat{\beta}_2\)	\(\widehat{\beta}_3\)	\(\widehat{\beta}_4\)	\(\widehat{\beta}_5\)
86596	-4771	-13473	14560	49160	-89

Interprétation de coefficients des données du collège

• L’ordonnée à l’origine \(\beta_0\) correspond au salaire moyen d’un professeur adjoint (un homme) qui vient de compléter ses études et qui travaille dans un domaine appliqué: on estime ce salaire à \(\widehat{\beta}_0=86596\) dollars.
• toutes choses étant égales par ailleurs (même domaine, échelon et années depuis le dernier diplôme), l’écart de salaire entre un homme et un femme est estimé à \(\widehat{\beta}_1=-4771\) dollars.
• ceteris paribus, un(e) professeur(e) qui oeuvre dans un domaine théorique gagne \(\beta_2\) dollars de plus qu’une personne du même sexe dans un domaine appliqué; on estime cette différence à \(-13473\) dollars.
• ceteris paribus, la différence moyenne de salaire entre professeurs adjoints et aggrégés est estimée à \(\widehat{\beta}_3=14560\) dollars.
• ceteris paribus, la différence moyenne de salaire entre professeurs adjoints et titulaires est de \(\widehat{\beta}_4=49160\) dollars.
• au sein d’un même échelon, chaque année supplémentaire de service mène à une augmentation de salaire annuelle moyenne de \(\widehat{\beta}_5=-89\) dollars.

Estimation des paramètres

Considérons une matrice de modèle \(\mathbf{X}\) et une équation pour la moyenne du modèle linéaire de la forme \(\mathsf{E}(Y_i) = \mathbf{x}_i\boldsymbol{\beta}\).

Le modèle linéaire comprend

• \(p+1\) paramètres pour la moyenne, \(\boldsymbol{\beta}\), et
• un paramètre de variance \(\sigma^2\).

Problème des moindres carrés ordinaires

Nous voulons trouver le vecteur de paramètres \(\boldsymbol{\beta} \in \mathbb{R}^{p+1}\) qui minimise l’erreur quadratique moyenne, c’est-à-dire la distance verticale entre les valeurs ajustées \(\widehat{y}_i=\mathbf{x}_i\widehat{\boldsymbol{\beta}}\) et les observations \(y_i\).

Le problème d’optimisation est \[\begin{align*} \widehat{\boldsymbol{\beta}}&=\mathrm{arg min}_{\boldsymbol{\beta} \in \mathbb{R}^{p+1}}\sum_{i=1}^n (y_i-\mathbf{x}_i\boldsymbol{\beta})^2 \\&=(\boldsymbol{y}-\mathbf{X}\boldsymbol{\beta})^\top(\boldsymbol{y}-\mathbf{X}\boldsymbol{\beta}). \end{align*}\]

Estimateur des moindres carrés ordinaires

Si la matrice \(n \times p\) \(\mathbf{X}\) est de plein rang, c’est-à-dire que ses colonnes ne sont pas des combinaisons linéaires les unes des autres, la forme quadratique \(\mathbf{X}^\top \mathbf{X}\) est inversible et nous obtenons \[ \widehat{\boldsymbol{\beta}} = \left(\mathbf{X}^\top \mathbf{X}\right)^{-1}\mathbf{X}^\top \boldsymbol{y}. \qquad(1)\] Cette formule est celle de l’estimateur des moindres carrés ordinaires (MCO). Puisqu’il existe une solution analytique, aucune optimisation numérique n’est requise.

Décomposition orthogonale

• Le vecteur de valeurs ajustées \(\widehat{\boldsymbol{y}} =\mathbf{X} \widehat{\boldsymbol{\beta}} = \mathbf{H}_{\mathbf{X}}\boldsymbol{y}\) est la projection de la variable réponse \(\boldsymbol{y}\) dans l’espace linéaire engendré par les colonnes de \(\mathbf{X}\).
• Les résidus ordinaires \(\boldsymbol{e} = \boldsymbol{y} - \widehat{\boldsymbol{y}}\) sont la différence entre observations et prédictions.
• On peut montrer que les produit scalaire entre résidus et valeurs ajustés, \[\widehat{\boldsymbol{y}}^\top \boldsymbol{e} = \sum_{i=1}^n \widehat{y}_ie_i=0,\] ce qui implique que la corrélation entre les deux vecteurs est nulle, \(\widehat{\mathsf{cor}}(\widehat{\boldsymbol{y}}, \boldsymbol{e})=0\)
  • De manière équivalente, \(\mathbf{X}^\top\boldsymbol{e}=\boldsymbol{0}_{p+1}\).
  • La moyenne empirique de \(\boldsymbol{e}\) est zéro si le vecteur constant \(\mathbf{1}_n\) est dans l’espace linéaire engendré par \(\mathbf{X}\).

Représentation graphique des résidus

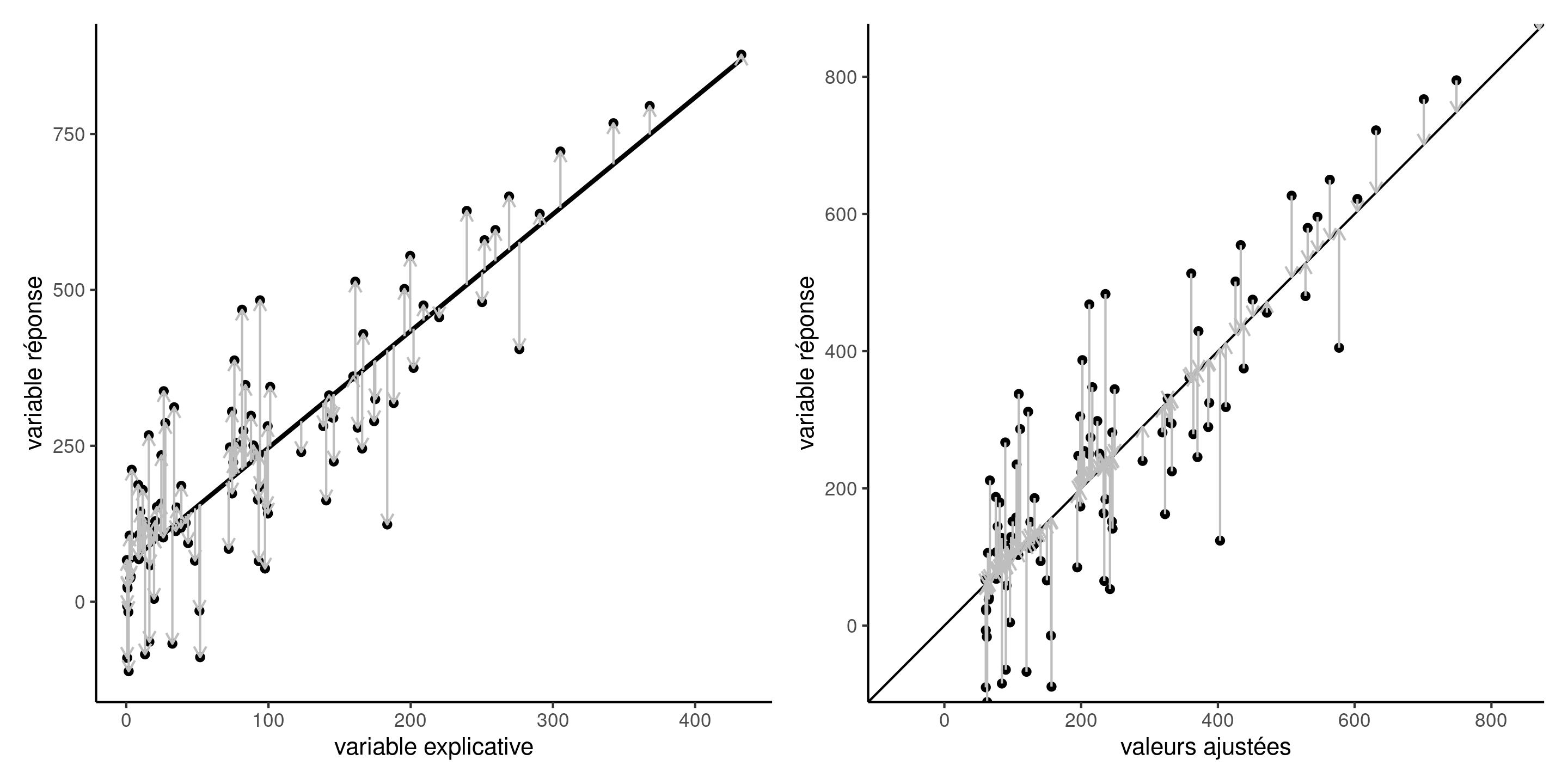
Figure 4: Résidus ordinaires \(e_i\) (vecteurs verticaux) ajoutés à la droite de régression passant dans le plan \((x, y)\) (gauche) et ajustement de la réponse \(y_i\) contre les valeurs ajustées \(\widehat{y}_i\). La droite des moindres carrés ordinaires minimise la distance au carré des résidus ordinaires.

EMV de la moyenne du modèle linéaire normal

Si \(Y_i \sim \mathsf{normale}(\mathbf{x}_i\boldsymbol{\beta}, \sigma^2)\) et les données sont indépendantes, la log-vraisemblance du modèle linéaire normal s’écrit \[\begin{align*} \ell(\boldsymbol{\beta}, \sigma)&\propto-\frac{n}{2} \ln (\sigma^2) -\frac{(\boldsymbol{y}-\mathbf{X}\boldsymbol{\beta})^\top(\boldsymbol{y}-\mathbf{X}\boldsymbol{\beta})}{2\sigma^2}. \end{align*}\]

Maximiser la log-vraisemblance par rapport à \(\boldsymbol{\beta}\) équivaut à minimiser la somme du carré des erreurs \(\sum_{i=1}^n (y_i - \mathbf{x}_i\boldsymbol{\beta})^2\), indépendamment de la valeur de \(\sigma\).

On recouvre l’estimateur des moindres carrés ordinaires \(\widehat{\boldsymbol{\beta}}\).

EMV de la variance

Pour obtenir les EMV de \(\sigma^2\), on se sert de la log vraisemblance profilée. En excluant les termes constants qui ne dépendent pas de \(\sigma^2\), \[\begin{align*} \ell_{\mathrm{p}}(\sigma^2) &\propto-\frac{1}{2}\left\{n\ln\sigma^2+\frac{1}{\sigma^2}(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol{\beta}})^\top(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol{\beta}})\right\}. \end{align*}\]

En différenciant chaque terme par rapport à \(\sigma^2\) et en fixant le gradient à zéro, on obtient \[\begin{align*} \frac{\partial \ell_{\mathrm{p}}(\sigma^2)}{\partial \sigma^2} = -\frac{n}{2\sigma^2} + \frac{(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol{\beta}})^\top(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol{\beta}})}{2\sigma^4} = 0 \end{align*}\]

EMV pour la variance

On déduit que l’estimateur du maximum de vraisemblance est la moyenne des carrés des résidus, \[\begin{align*} \widehat{\sigma}^2&=\frac{1}{n}(\boldsymbol{Y}-\mathbf{X}\hat{\boldsymbol{\beta}})^\top(\boldsymbol{Y}-\mathbf{X}\hat{\boldsymbol{\beta}})\\&= \frac{1}{n} \sum_{i=1}^n (y_i - \mathbf{x}_i\widehat{\boldsymbol{\beta}})^2= \frac{\mathsf{SC}_e}{n}; \end{align*}\]

L’estimateur sans biais habituel de \(\sigma^2\) calculé par le logiciel est \[S^2=\mathsf{SC}_e/(n-p-1),\] où le dénominateur est la taille de l’échantillon moins le nombre de paramètres de la moyenne.

Information observée pour le modèle linéaire normal

Les entrées de la matrice d’information observée sont \[\begin{align*} -\frac{\partial^2 \ell(\boldsymbol{\beta}, \sigma^2)}{\partial \boldsymbol{\beta}\partial \boldsymbol{\beta}^\top} &= \frac{1}{\sigma^2} \frac{\partial \mathbf{X}^\top(\boldsymbol{y}-\mathbf{X}\boldsymbol{\beta})}{\partial \boldsymbol{\beta}^\top} = \frac{\mathbf{X}^\top\mathbf{X}}{\sigma^2}\\ -\frac{\partial^2 \ell(\boldsymbol{\beta}, \sigma^2)}{\partial \boldsymbol{\beta}\partial \sigma^2} &=- \frac{\mathbf{X}^\top(\boldsymbol{y}-\mathbf{X}\boldsymbol{\beta})}{\sigma^4}\\ -\frac{\partial^2 \ell(\boldsymbol{\beta}, \sigma^2)}{\partial (\sigma^2)^2} &= -\frac{n}{2\sigma^4} + \frac{(\boldsymbol{y}-\mathbf{X}\boldsymbol{\beta})^\top(\boldsymbol{y}-\mathbf{X}\boldsymbol{\beta})}{\sigma^6}. \end{align*}\]

Matrices d’information du modèle linéaire normal

Si on évalue l’information observée aux EMV, \[\begin{align*} j(\widehat{\boldsymbol{\beta}}, \widehat{\sigma}^2) = \begin{pmatrix} \frac{\mathbf{X}^\top\mathbf{X}}{\widehat{\sigma^2}} & \boldsymbol{0}_{p+1} \\ \boldsymbol{0}_{p+1}^\top & \frac{n}{2\widehat{\sigma^4}} \end{pmatrix} \end{align*}\] car \(\widehat{\sigma}^2=\mathsf{SC}_e/n\) et les résidus sont orthogonaux à la matrice du modèle.

Puisque \(\mathsf{E}(Y \mid \mathbf{X})=\mathbf{X}\boldsymbol{\beta}\), l’information de Fisher est \[\begin{align*} i(\boldsymbol{\beta}, \sigma^2) = \begin{pmatrix} \frac{\mathbf{X}^\top\mathbf{X}}{\sigma^2} & \boldsymbol{0}_{p+1} \\ \boldsymbol{0}_{p+1}^\top & \frac{n}{2\sigma^4} \end{pmatrix} \end{align*}\]

Remarques

Puisque la loi asymptotique de l’estimateur est normale, les EMV de \(\sigma^2\) et \(\boldsymbol{\beta}\) sont asymptotiquement indépendants car leur corrélation asymptotique est nulle.

Pourvu que la matrice carrée \((p+1)\), \(\mathbf{X}^\top\mathbf{X}\) soit inversible, la variance asymptotique des estimateurs est

• \(\mathsf{Var}(\widehat{\boldsymbol{\beta}})=\sigma^2(\mathbf{X}^\top\mathbf{X})^{-1}\),
• \(\mathsf{Var}(\widehat{\sigma}^2) = 2\sigma^4/n\).

Références

Baumann, James F., Nancy Seifert-Kessell, et Leah A. Jones. 1992. « Effect of Think-Aloud Instruction on Elementary Students’ Comprehension Monitoring Abilities ». Journal of Reading Behavior 24 (2): 143‑72. https://doi.org/10.1080/10862969209547770.

Lee, Kiljae, et Jungsil Choi. 2019. « Image-text inconsistency effect on product evaluation in online retailing ». Journal of Retailing and Consumer Services 49: 279‑88. https://doi.org/10.1016/j.jretconser.2019.03.015.

Moon, Alice, et Eric M VanEpps. 2023. « Giving Suggestions: Using Quantity Requests to Increase Donations ». Journal of Consumer Research 50 (1): 190‑210. https://doi.org/10.1093/jcr/ucac047.