Modélisation statistique

05. Modèles linéaires (géométrie)

Léo Belzile, HEC Montréal

2024

Géométrie des colonnes

L’équation du modèle linéaire est \[\boldsymbol{Y} = \underset{\vphantom{é}\text{moyenne } \boldsymbol{\mu}}{\vphantom{y}\mathbf{X}\boldsymbol{\beta}} + \underset{\text{aléa}}{\vphantom{y}\boldsymbol{\varepsilon}}\] et supposons que $\mathsf{E}(\boldsymbol{\varepsilon} \mid \mathbf{X})= \boldsymbol{0}_n$ et $\mathsf{Va}(\boldsymbol{\varepsilon} \mid \mathbf{X}) = \sigma^2\mathbf{I}_n$. La décomposition du modèle en termes de résidus et de valeurs ajustées est \[\begin{align*} \underset{\text{observations}}{\boldsymbol{y}} = \underset{\text{valeurs ajustées}}{\widehat{\boldsymbol{y}}} + \underset{\text{résidus}}{\vphantom{y}\boldsymbol{e}} \end{align*}\]

Matrices de projection

Pour une matrice de modèle de dimension $n\times (p+1)$, le sous-espace vectoriel engendré par les colonnes de $\mathbf{X}$ est \[\begin{align*} \mathcal{S}(\mathbf{X}) =\{\mathbf{X}\boldsymbol{a}, \boldsymbol{a} \in \mathbb{R}^{p+1}\} \end{align*}\]

On peut écrire les valeurs ajustées comme la projection du vecteur réponse $\boldsymbol{y}$ dans sous-espace vectoriel engendré de $\mathbf{X}$, \[\begin{align*} \underset{\text{valeurs ajustées}}{\widehat{\boldsymbol{y}}} = \underset{\substack{\text{matrice du modèle $\times$}\\\text{estimateur des MCO}}}{\mathbf{X} \widehat{\boldsymbol{\beta}}} = \underset{\text{matrice de projection}}{\mathbf{X}(\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{X}^\top}\boldsymbol{y} = \mathbf{H}_{\mathbf{X}}\boldsymbol{y} \end{align*}\] où $\mathbf{H}_{\mathbf{X}} = \mathbf{X}(\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{X}^\top$ est une matrice de projection orthogonale.

$\mathbf{H}_{\mathbf{X}}$ est une matrice symmétrique $n \times n$ de rang $p+1$.
Une matrice de projection orthogonale est telle que $\mathbf{H}_{\mathbf{X}}\mathbf{H}_{\mathbf{X}} = \mathbf{H}_{\mathbf{X}}$ et $\mathbf{H}_{\mathbf{X}} = \mathbf{H}_{\mathbf{X}}^\top$.

Visualisation de la géométrie

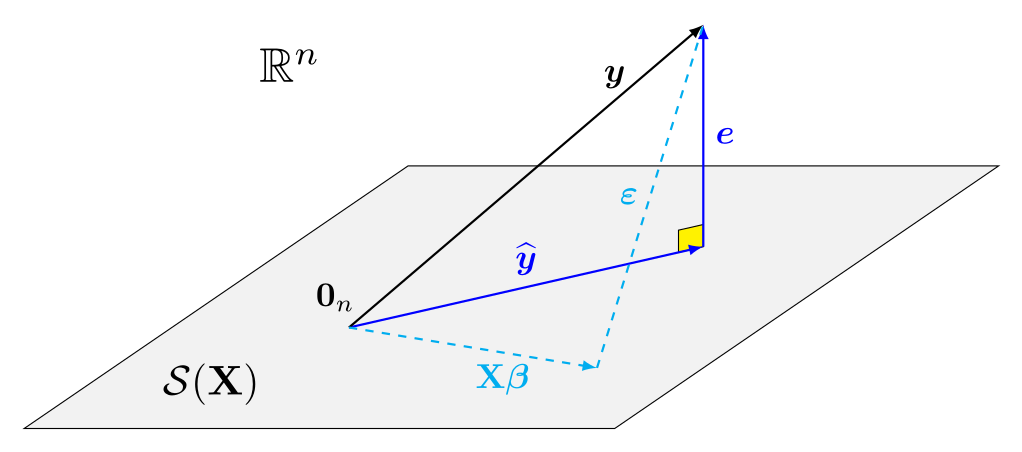
Conséquence de l’orthogonalité

La représentation et les propriétés géométriques ont des corollaires importants pour l’inférence et la constructions de diagnostics.

Si $\mathbf{1}_n \in \mathcal{S}(\mathbf{X})$ (par ex., l’ordonnée à l’origine est incluse dans $\mathbf{X}$), la moyenne empirique de $\boldsymbol{e}$ est nulle.
Les valeurs ajustées $\widehat{\boldsymbol{y}}$ et les résidus ordinaires $\boldsymbol{e}$ ne sont pas corrélés.
Idem pour toute colonne de $\mathbf{X}$, puisque $\mathbf{X}^\top\boldsymbol{e}=\boldsymbol{0}_{p+1}$.

data(college, package = "hecmodstat")
mod <- lm(salaire ~ sexe + echelon + service, data = college)
# Corrélations nulles
cor(resid(mod), model.matrix(mod))[-1]
## [1]  2.3e-16 -4.2e-17 -1.9e-16  7.1e-17
cor(resid(mod), fitted(mod))
## [1] 1.7e-16
# Moyenne des résidus nulle
mean(resid(mod))
## [1] 3.2e-16

Diagnostics graphiques

Une régression linéaire simple de $\widehat{\boldsymbol{y}}$ (ou de toute colonne de $\mathbf{X}$) avec réponse $\boldsymbol{e}$ a une ordonnée à l’origine et une pente de zéro.

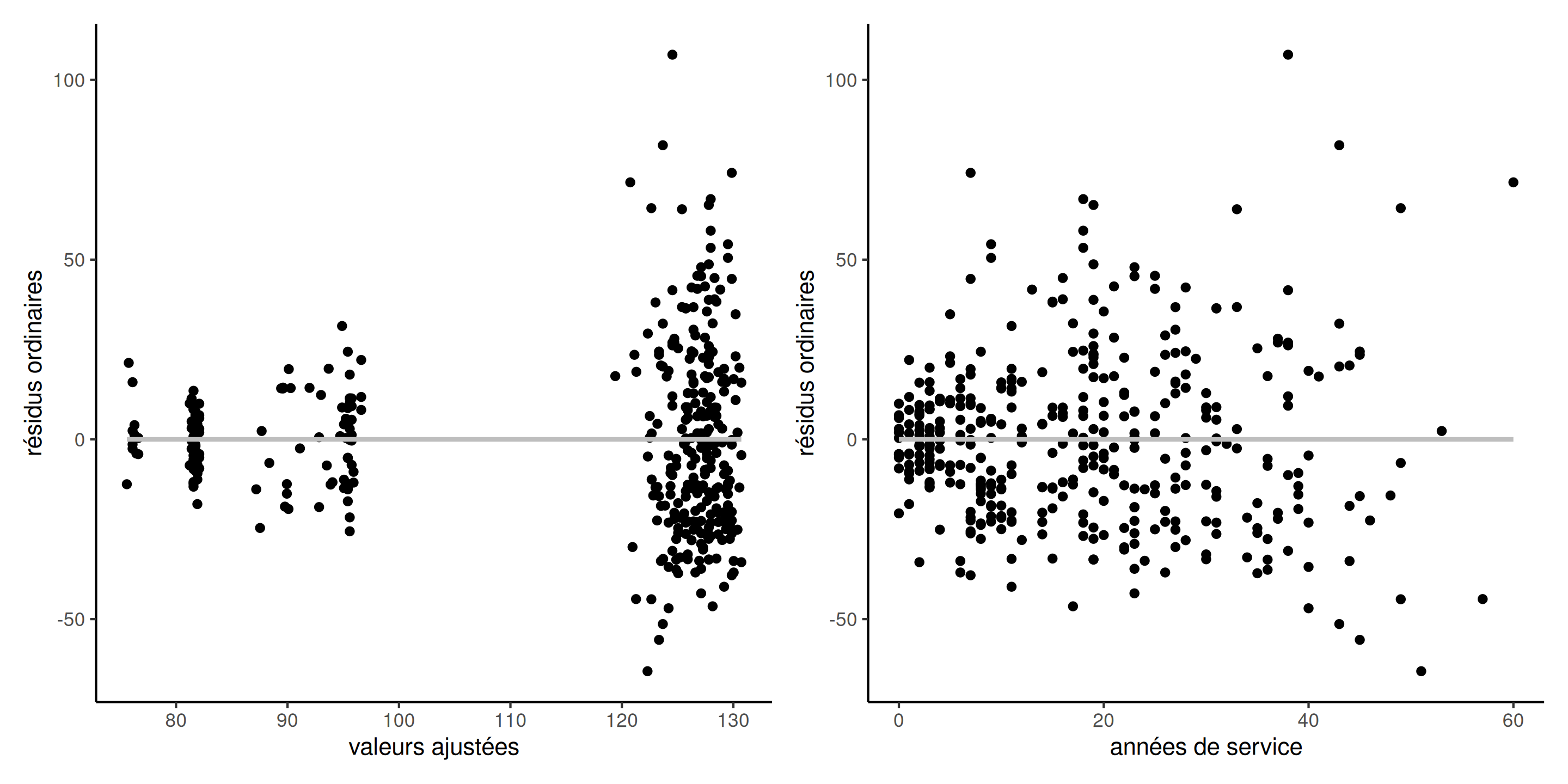
Figure 1: Diagramme des résidus versus valeurs ajustées (gauche), et variable explicative service (droite) pour le modèle avec les données college, L’ordonnée à l’origine et la pente sont nulles.

Les tendances résiduelles dues à des interactions, des termes nonlinéaires, etc. seront visibles dans les diagrammes.

Invariance

Les valeurs ajustées $\widehat{y}_i$ pour deux matrices de modèle $\mathbf{X}_a$ et $\mathbf{X}_b$sont les mêmes si elles engendrent le même sous-espace vectoriel, $\mathcal{S}(\mathbf{X}_a) = \mathcal{S}(\mathbf{X}_b)$.

modA <- lm(salaire ~ sexe + echelon + service, data = college)
modB <- lm(salaire ~ 0 + sexe + echelon + service, # Enlever l'ordonnée à l'origine
           data = college |> 
            dplyr::mutate(service = scale(service)), # Centrer-réduire une variable
           contrasts = list(echelon = contr.sum)) # changer la paramétrisation
head(model.matrix(modA), n = 3L)
##   (Intercept) sexehomme echelonaggrege echelontitulaire service
## 1           1         1              0                1      18
## 2           1         1              0                1      16
## 3           1         1              0                0       3
head(model.matrix(modB), n = 3L)
##   sexefemme sexehomme echelon1 echelon2 service
## 1         0         1       -1       -1    0.03
## 2         0         1       -1       -1   -0.12
## 3         0         1        1        0   -1.12
# Invariance du modèle
isTRUE(all.equal(fitted(modA), fitted(modB)))
## [1] TRUE

Loi des aléas

En définissant les résidus comme \[\boldsymbol{E}=(\mathbf{I}-\mathbf{H}_{\mathbf{X}})\boldsymbol{Y},\] il en découle si $Y_i \sim \mathsf{normale}(\mathbf{x}_i\boldsymbol{\beta}, \sigma^2)$ que

Marginalement, $E_i \sim \mathsf{normale}\{0, \sigma^2(1-h_{ii})\}$.
Les résidus sont hétéroscédastiques (de variance différente). Leur variance dépend des éléments diagonaux de la “matrice chapeau” $\mathbf{H}_{\mathbf{X}}$, soit $\{h_{ii}\}$ pour $(i=1, \ldots, n)$.
Les résidus ordinaires sont linéairement dépendants (il y a $n-p-1$ composantes indépendantes, puisque $\mathbf{I}-\mathbf{H}_{\mathbf{X}}$ est une matrice de rang $n-p-1$).
On peut montrer que $\mathsf{Cov}(e_i, e_j) = -\sigma^2h_{ij}$: les résidus sont corrélés.

Estimation de la variance

Si on estime $\sigma^2$ par $S^2$, on introduit une dépendance additionnelle puisque $S^2 = \sum_{i=1}^n e_i^2/(n-p-1)$, donc $e_i$ apparaît dans la formule de la variance empirique…
On considère plutôt $S^2_{-i}$, l’estimateur obtenu en calculant la somme du carré des erreurs de la régression avec $n-1$ observations, en excluant la ligne $i$.
Une formule explicite existe en terme de $S^2$ et de $h_{ii}$, (pas besoin de recalculer $n$ régressions linéaires!), soit \[S^2_{-i} = \frac{(n-p-1)S^2 - e_i^2/(1-h_{ii})}{n-p-2}.\]

Résidus studentisés externes

Les résidus résidus studentisés dits externe sont définis comme \[r_i = \frac{e_i}{S_{-i}(1-h_{ii})^{1/2}}\] Dans R, on les obtient via rstudent.
Leur loi marginale est $R_i \sim \mathsf{Student}(n-p-2)$.
$R_1, \ldots, R_n$ ne sont en revanche pas indépendants.

Effet levier

Les éléments diagonaux de la matrice chapeau $h_{ii} = \partial \widehat{y}_i/\partial y_i$ représentent l’effet levier d’une observation.
Le levier nous indique à quel point une observation impacte l’ajustement. Les valeurs sont bornées entre $1/n$ et $1$.
La somme des effets leviers est $\sum_{i=1}^n h_{ii}=p+1$: dans un bon devis, chaque point a une contribution moyenne égale avec un poids de $(p+1)/n$.
Les points qui ont un effet levier important sont typiquement ceux qui ont des combinaisons inhabituelles de variables explicatives.
Une condition pour que l’estimateur des MCO $\widehat{\boldsymbol{\beta}}$ soit convergent est que $\max_{i=1}^n h_{ii} \to 0$ à mesure que $n \to \infty$: aucune observation ne doit dominer l’ajustement.

Valeurs influentes vs aberrances

Il est important de distinguer entre une valeur influente (qui une combinaison de $\mathbf{x}$ inhabituelle, loin de la moyenne), et une valeur aberrante (valeur inhabituelle de $y$).

Si une valeur aberrante a un effet de levier élevé (typiquement $h_{ii}>2(p+1)/n$, c’est problématique.

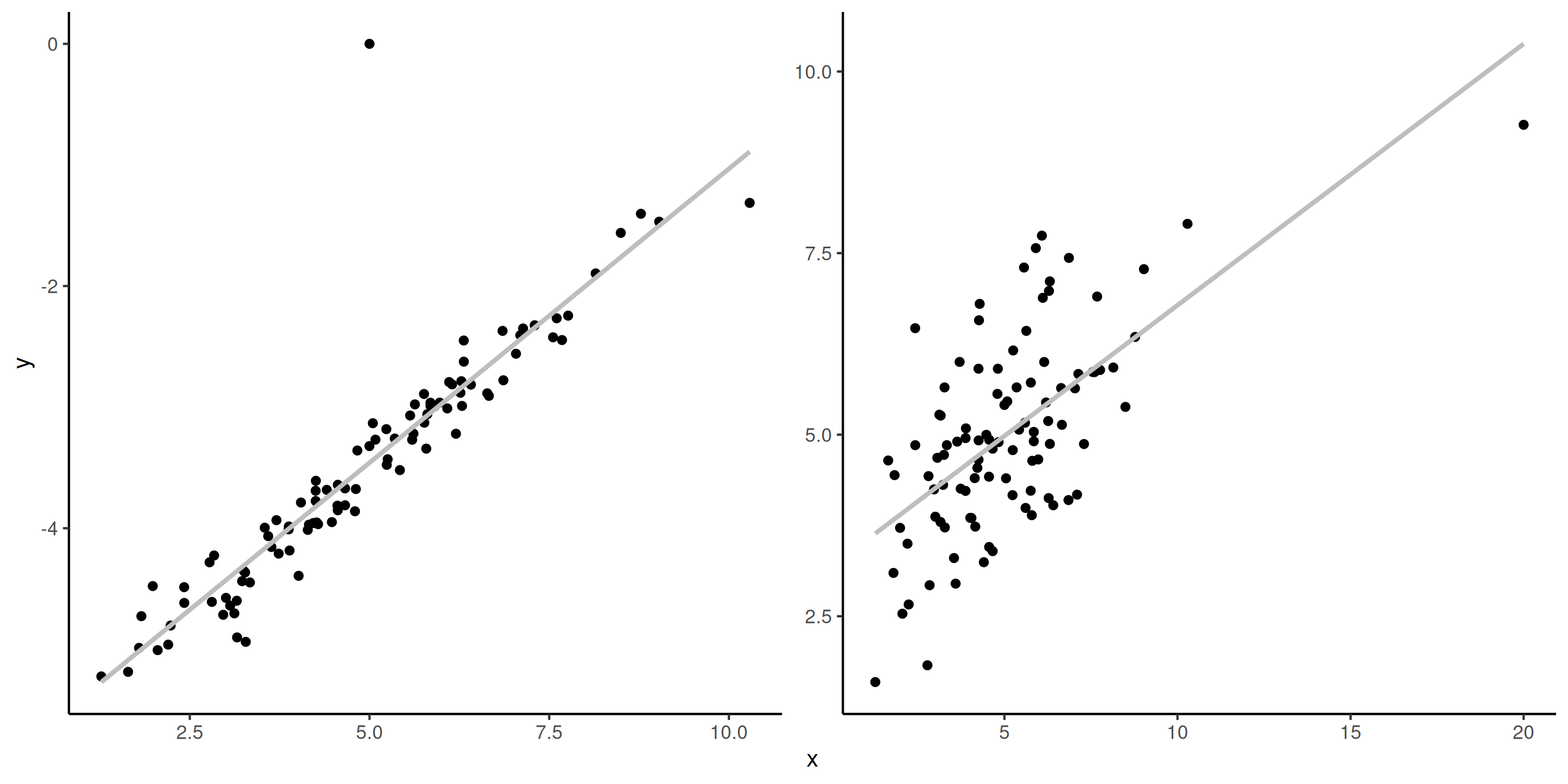
Figure 2: Valeur aberrante (gauche) et observation influente (droite, valeur de $x$ la plus à droite).

Distance de Cook

La distance de Cook d’une observation mesure l’effet sur l’ajustement de l’observation $i$: on estime les MCO de la régression sans l’observation $i$, disons $\widehat{\boldsymbol{\beta}}_{-i}$, pour obtenir les prédictions des $n$ observations, disons $\widehat{\boldsymbol{y}}_{-i}=\mathbf{X}\widehat{\boldsymbol{\beta}}_{-i}$. Alors

\[ C_i =\frac{1}{(p+1)S^2}\left(\widehat{\boldsymbol{y}}-\widehat{\boldsymbol{y}}_{-i}\right)^\top \left(\widehat{\boldsymbol{y}}-\widehat{\boldsymbol{y}}_{-i}\right)= \frac{r_i^2h_{ii}}{(p+1)(1-h_{ii})}. \]

La distance Cook est grande quand $r_i$ est grande et/ou $h_{ii}$ est grand.