Modélisation statistique

05. Modèles linéaires (coefficient de détermination)

Léo Belzile, HEC Montréal

2024

Corrélation linéaire de Pearson

La corrélation linéaire mesure la force de la relation linéaire entre deux variables aléatoires \(X\) et \(Y\). \[\begin{align*} \rho= \mathsf{cor}(X, Y) = \frac{{\mathsf{Co}}(X,Y)}{\sqrt{{\mathsf{Va}}(X){\mathsf{Va}}(Y)}}. \end{align*}\]

  • La corrélation satisfait \(\rho \in [-1, 1]\).
  • \(|\rho|=1\) si et seulement si les \(n\) observations sont alignées.
  • Plus \(|\rho|\) est grande, moins les points sont dispersés.

Propriétés de la corrélation linéaire

Le signe de la corrélation détermine le signe de la pente (à la baisse pour \(\rho\) négatif, à la hausse pour \(\rho\) positive).

Si \(\rho>0\) (ou \(\rho<0\)), les deux variables sont positivement (négativement) associées, ce qui veut dire que \(Y\) augmente (diminue) en moyenne avec \(X\).

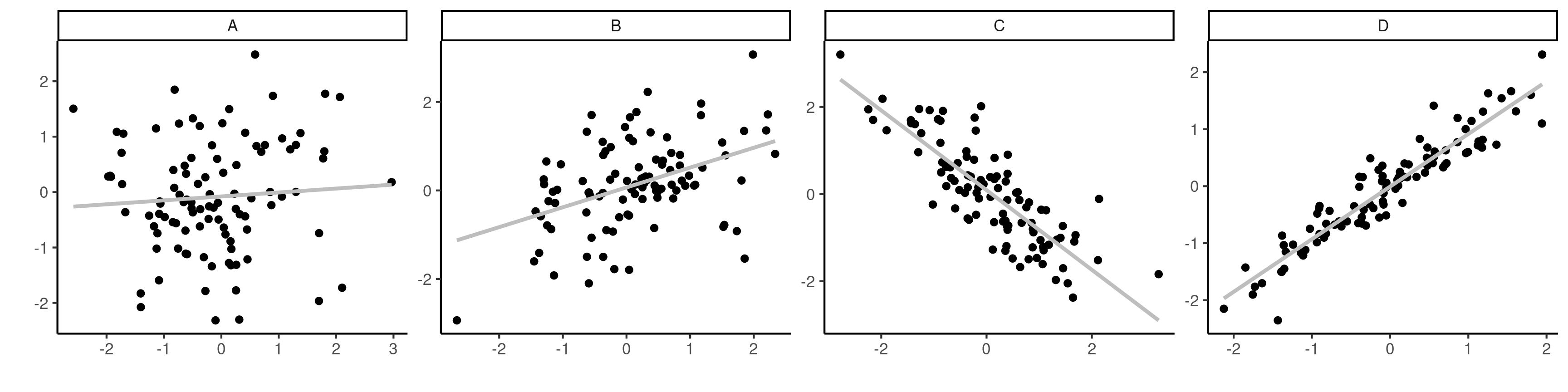
Figure 1: Nuages de points d’observations avec des corrélations de \(0.1\), \(0.5\), \(-0.75\) et \(0.95\) de \(A\) jusqu’à \(D\).

Corrélation et indépendance

  • Les variables indépendantes ont une corrélation nulle (mais pas nécessairement l’inverse).
  • Une corrélation linéaire de zéro indique seulement qu’il n’y a pas de dépendance linéaire entre les variables.

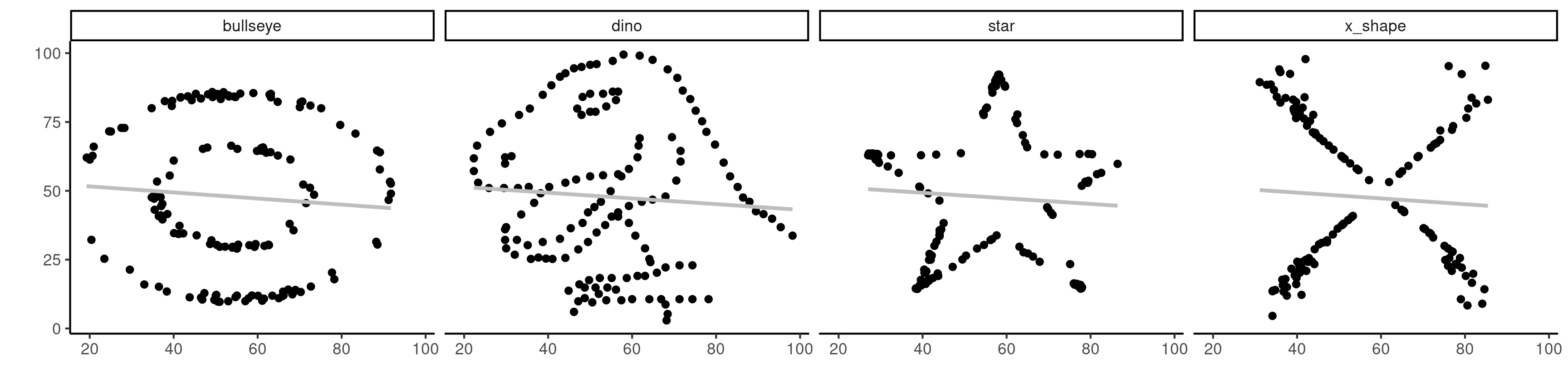
Figure 2: Quatre jeux de données avec des statistiques descriptives identiques, dont une corrélation linéaire de \(-0.06\).

Décomposition de la somme des carrés

Si on considère le modèle avec seulement une ordonnée à l’origine, la valeur ajustée pour \(Y\) est la moyenne globale et la somme des observations centrées au carré est \[\begin{align*} \mathsf{SC}_c=\sum_{i=1}^n (Y_i-\overline{Y})^2 \end{align*}\] où \(\overline{Y}\) représente la valeur ajustée du modèle.

Si on inclut \(p\) variables explicatives, on obtient \[\begin{align*} \mathsf{SC}_e=\sum_{i=1}^n (Y_i-\widehat{Y}_i)^2 \end{align*}\] Si on inclut plus de variables, \(\mathsf{SC}_e\) ne peut augmenter.

Pourcentage de variance expliquée

Considérons la somme du carré des résidus des deux modèles:

  • \(\mathsf{SC}_c\) pour le modèle avec seulement l’ordonnée à l’origine.
  • \(\mathsf{SC}_e\) pour le modèle de régression linéaire avec matrice du modèle \(\mathbf{X}\).

La différence \(\mathsf{SC}_c-\mathsf{SC}_e\) est la réduction de l’erreur associée à l’ajout de covariables de \(\mathbf{X}\) dans le modèle \[\begin{align*} R^2=\frac{\mathsf{SC}_c-\mathsf{SC}_e}{\mathsf{SC}_c} \end{align*}\] Ainsi, le coefficient \(R^2\) représente la proportion de variance de \(Y\) expliquée par \(\mathbf{X}\).

Coefficient de détermination

On peut démontrer que le coefficient de détermination \(R^2\) est le carré de la corrélation linéaire entre la variable réponse \(\boldsymbol{y}\) et les valeurs ajustées \(\widehat{\boldsymbol{y}}\), \[R^2 = \mathsf{cor}^2(\boldsymbol{y}, \widehat{\boldsymbol{y}}).\]

data(college, package = "hecmodstat")
mod <- lm(salaire ~ sexe + echelon + service, data = college)
summary(mod)$r.squared # R-carré dans la sortie
## [1] 0.4
y <- college$salaire # vecteur de variables réponse
yhat <- fitted(mod) # valeurs ajustées ychapeau
cor(y, yhat)^2  # coefficient R-carré
## [1] 0.4
  • \(R^2\) prend toujours des valeurs entre \(0\) et \(1\).
  • \(R^2\) n’est pas une mesure de la qualité de l’ajustement: le coefficient est non-décroissant à mesure que la dimension de \(\mathbf{X}\) augmente. Autrement dit, le plus de variables explicatives on ajoute, le plus grand le \(R^2\).