| lognutilisateur | celcius | farenheit | rfarenheit |
|---|---|---|---|
| 7.36 | 1.5 | 34.7 | 35 |
| 8.06 | 0.2 | 32.4 | 32 |
| 8.67 | 6.8 | 44.2 | 44 |
| 8.58 | 10.1 | 50.2 | 50 |
| 8.70 | 10.3 | 50.5 | 51 |
Modélisation statistique
06. Modèles linéaires (colinéarité)
2024
Colinéarité
- La colinéarité (ou multicolinéarité) sert à décrire le cas de figure où une variable explicative est fortement corrélée avec une combinaison linéaire des autres covariables.
- Une conséquence nuisible de la colinéarité est la perte de précision dans l’estimation des paramètres, et donc l’augmentation des erreurs-type des paramètres.
Bixi et colinéarité
On s’intéresse au nombre de locations quotidiennes de Bixi entre 2014 et 2019 en fonction de la température de l’aéroport voisin de Dorval, enregistrée à 16h.
Invariance linéaire
Soit le log du nombre quotidien de locations de Bixi en fonction de la température en degrés Celcius et Farenheit (et la température en \({}^{\circ}\)F arrondie au degré près). Si on ajuste le modèle linéaire \[\begin{align*} \texttt{lognutilisateur} = \beta_0 + \beta_{\texttt{c}} \texttt{celcius} + \beta_{\texttt{f}} \texttt{farenheit} + \varepsilon. \end{align*}\]
- L’interprétation de \(\beta_{\texttt{c}}\) est “le facteur d’augmentation du nombre de locations quotidiennes quand la température croît de \(1{}^{\circ}\)C, tout en gardant la température en Farenheit constante”
- Or, les deux unités de températures sont liées par la relation linéaire \[1.8 \texttt{celcius} + 32 = \texttt{farenheit}.\]
Le noeud du problème
Supposons que le vrai effet (fictif) de la température sur le log du nombre de locations de vélo est \[\begin{align*} \mathsf{E}(\texttt{lognutilisateur} \mid \cdot) = \alpha_0+ \alpha_1 \texttt{celcius}. \end{align*}\]
Les coefficients du modèle qui n’inclut que la température Farenheit sont donc \[\begin{align*} \mathsf{E}(\texttt{lognutilisateur} \mid \cdot)= \gamma_0 + \gamma_1\texttt{farenheit}, \end{align*}\] avec \(\alpha_0 = \gamma_0 + 32\gamma_1\) et \(1.8\gamma_1 = \alpha_1\).
| coef. | erreur-type | |
|---|---|---|
| cst | 8.844 | 0.028 |
| Celcius | 0.049 | 0.001 |
| coef. | erreur-type | |
|---|---|---|
| cst | 7.981 | 0.051 |
| Farenheit | 0.027 | 0.001 |
Colinéarité exacte
Les paramètres du modèle postulé avec les deux variables, \[\begin{align*} \texttt{lognutilisateur} = \beta_0 + \beta_{\texttt{c}} \texttt{celcius} + \beta_{\texttt{f}} \texttt{farenheit} + \varepsilon, \end{align*}\] ne sont pas identifiables: n’importe laquelle combinaison linéaire des deux solutions donne le même modèle ajusté.
C’est la même raison pour laquelle on n’inclut que \(K-1\) variables indicatrices pour un facteur à \(K\) niveaux si le modèle inclut l’ordonnée à l’origine.
Solutions multiples
# Colinéarité exacte détectée
modlin3_bixicol <- lm(lognutilisateur ~ celcius + farenheit, data = bixicol)
summary(modlin3_bixicol)
##
## Call:
## lm(formula = lognutilisateur ~ celcius + farenheit, data = bixicol)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.5539 -0.2136 0.0318 0.2400 0.8256
##
## Coefficients: (1 not defined because of singularities)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 8.84433 0.02819 313.7 <2e-16 ***
## celcius 0.04857 0.00135 35.9 <2e-16 ***
## farenheit NA NA NA NA
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.354 on 1182 degrees of freedom
## Multiple R-squared: 0.522, Adjusted R-squared: 0.521
## F-statistic: 1.29e+03 on 1 and 1182 DF, p-value: <2e-16Estimation avec quasi-colinéarité parfaite
modlin4_bixicol <- lm(lognutilisateur ~ celcius + rfarenheit, data = bixicol)
summary(modlin4_bixicol)
##
## Call:
## lm(formula = lognutilisateur ~ celcius + rfarenheit, data = bixicol)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.5467 -0.2135 0.0328 0.2407 0.8321
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 9.5551 1.1475 8.33 2.3e-16 ***
## celcius 0.0886 0.0646 1.37 0.17
## rfarenheit -0.0222 0.0359 -0.62 0.54
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.354 on 1181 degrees of freedom
## Multiple R-squared: 0.522, Adjusted R-squared: 0.521
## F-statistic: 645 on 2 and 1181 DF, p-value: <2e-16Effets de la colinéarité
Règle générale, la colinéarité a les impacts suivants:
- Les estimés des coefficients changent drastiquement quand de nouvelles observations sont ajoutées au modèle, ou quand on ajoute/enlève des variables explicatives.
- Les erreurs-type des coefficients de la régression linéaire sont très élevées, parce que les coefficients ne peuvent pas être estimés précisément.
- Les paramètres individuels ne sont pas statistiquement significatifs, mais le test \(F\) pour l’effet global du modèle indiquera que certaines variables sont utiles.
Facteurs d’inflation de la variance
Pour une variable explicative donnée \(X_j\), définir \[\begin{align*} \mathsf{FIV}(j)=\frac{1}{1-R^2(j)} \end{align*}\] où \(R^2(j)\) est le coefficient de détermination \(R^2\) du modèle obtenu en régressant \({X}_j\) sur les autres variables explicatives.
\(R^2(j)\) donne la proportion de la variabilité de \(X_j\) expliquée par les autres variables.
Quand est-ce que la colinéarité est problématique?
Il n’y a pas de consensus mais, règle générale,
- \(\mathsf{FIV}(j) > 4\) sous-tend que \(R^2(j) >0.75\)
- \(\mathsf{FIV}(j) > 5\) sous-tend que \(R^2(j) >0.8\)
- \(\mathsf{FIV}(j) > 10\) sous-tend que \(R^2(j) >0.9\)
Colinéarité pour données Bixi
- La valeur de la statistique \(F\) pour le test de significativité globale (omise de la sortie) du modèle linéaire simple avec température Celcius est \(1290\) avec une valeur-\(p\) de moins de \(10^{-4}\); cela suggère que la température est un excellent prédicteur (\(5\)% d’augmentation du nombre d’utilisateurs pour chaque augmentation de \(1^{\circ}\)C).
- En revanche, dès qu’on inclut Celcius et Farenheit (arrondi au degré près), les coefficients individuels ne sont plus statistiquement significatifs à niveau \(5\%\).
- Qui plus est, le signe du coefficient de \(\texttt{rfarenheit}\) est différent de celui du modèle avec \(\texttt{farenheit}\)!
- Remarquez que les erreurs-type de Celcius sont \(47.79\) fois plus grandes dans le modèle avec les deux variables.
- Les facteurs d’inflation de la variance de \(\texttt{celcius}\) et \(\texttt{rfarenheit}\) sont de \(2283\), ce qui permet de diagnostiquer le problème.
Diagramme de régression partielle
Ce graphique montre la relation entre \(Y\) et \(X_j\) une fois que l’on a pris en compte les autres variables explicatives.
Construction
- Retirer la (ou les) colonne(s) de \(\mathbf{X}\) correspondant à la variable explicative \(X_j\); dénotons la matrice du modèle résultante \(\mathbf{X}_{-j}\).
- Ajuster une régression linéaire de \(\boldsymbol{Y}\) en fonction de \(\mathbf{X}_{-j}\),
- Ajuster une régression linéaire de \(\boldsymbol{X}_j\) en fonction de \(\mathbf{X}_{-j}\),
- Trace un nuage de point des résidus, avec la pente de régression \(\beta_j\).
Diagramme de régression partielle pour données Bixi
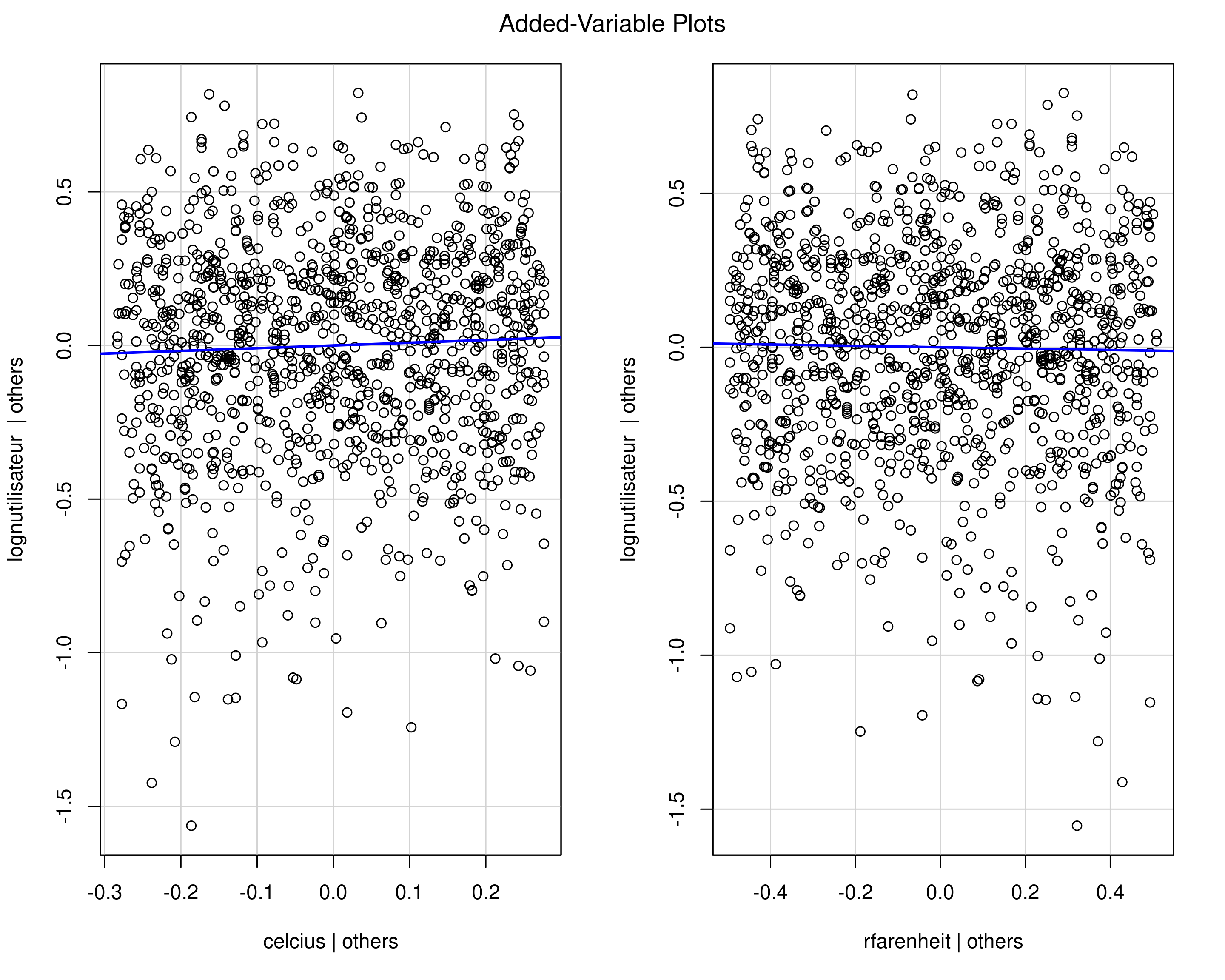
Figure 1: Diagramme de régression partiel pour les données Bixi. Puisque les données sont colinéaires, il n’y a pas de relation résiduelle si l’on prend en compte l’une ou l’autre des températures.
Exemple de diagramme de régression partielle
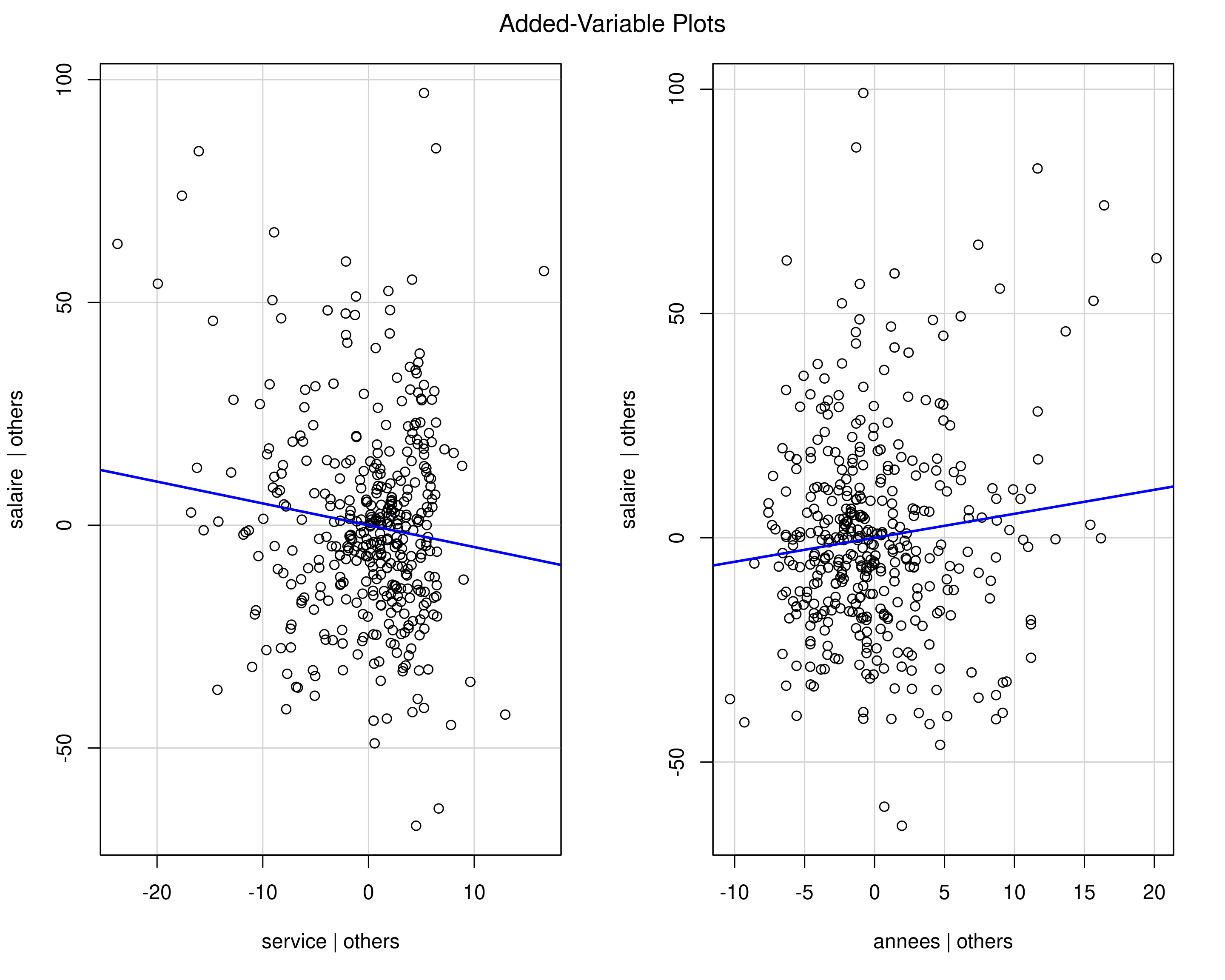
Figure 2: Diagramme de régression partielle pour le nombre d’années de service et le nombre d’années depuis le doctorat.
Facteur confondant
Un facteur confondant est une variable explicative \(C\) qui est associé à la variable réponse \(Y\) et qui est aussi corrélé à la variable explicative \(X\) d’intérêt.
flowchart TD
A("variable explicative") --> B("variable réponse")
C("facteur confondant") --> A & B
style A color:#FFFFFF, fill:#AA00FF, stroke:#AA00FF
style B color:#FFFFFF, stroke:#00C853, fill:#00C853
style C color:#FFFFFF, stroke:#2962FF, fill:#2962FF
Le facteur confondant \(C\) peut biaiser la relation observée entre une variable explicative \(X\) et la variable réponse \(Y\), et donc complique l’interprétation.
Exemple de facteur confondant
L’échelon académique des professeurs est corrélé avec le sexe, puisqu’il y a plus d’hommes que de femmes qui sont titulaires, et ces derniers sont mieux payés en moyenne. La variable echelon est un facteur confondant pour le sexe.
| coef. | erreur-type | stat | valeur p | |
|---|---|---|---|---|
| cst | 101.0 | 4.81 | 21.00 | < .001 |
| sexe [homme] | 14.1 | 5.06 | 2.78 | .006 |
| coef. | erreur-type | stat | valeur p | |
|---|---|---|---|---|
| cst | 76.64 | 4.43 | 17.29 | < .001 |
| sexe [homme] | 4.94 | 4.03 | 1.23 | .220 |
| échelon [agrégé] | 13.06 | 4.13 | 3.16 | .002 |
| échelon [titulaire] | 45.52 | 3.25 | 14.00 | < .001 |
Stratification et ajustement par régression
Quoi faire avec les facteurs confondants? On peut stratifier par différents niveaux du facteur confondant.
- Comparer le salaire séparément pour chaque échelon (chaque échelon représente une strate).
On peut aussi ajuster un modèle de régression avec plusieurs variables.
- On mesure ainsi l’effet de
sexe, en prenant en compte l’effet des autres variables explicatives.
Données expérimentales versus observationnelles
Les facteurs confondants sont essentiellement un problème pour les données observationnelles.
Dans un devis expérimental, un processus d’assignation aléatoire garantit que toutes les autres variables qui pourraient affecter \(Y\) sont équilibrées.
Dans ce cas, on peut tirer des conclusions sur l’effet de \(X\) sur \(Y\) sans ajuster pour les facteurs confondants.

Comment détecter la multicolinéarité
Si les variables sont exactement colinéaires, R éliminera celles qui sont superflues
Sinon, on peut examiner les corrélations entre variables, ou mieux encore les facteurs d’inflation de la variance.