Introduction à l’analyse factorielle
L’analyse factorielle consiste à résumer une matrice de covariance à l’aide d’un plus petit nombre de paramètres. Si on charge les données dans l’environnement, on remarque que toutes les variables correspondent à des échelles de Likert allant de un à cinq. Il n’est donc pas nécessaire de standardiser les données (en travaillant avec la matrice de corrélation).
library(hecmulti)
data(factor, package = "hecmulti")
# Statistiques descriptives
summary(factor)
#> x1 x2 x3 x4 x5
#> Min. :1.000 Min. :1.00 Min. :1.000 Min. :1.00 Min. :1.00
#> 1st Qu.:1.000 1st Qu.:1.00 1st Qu.:2.000 1st Qu.:2.00 1st Qu.:3.00
#> Median :2.000 Median :2.00 Median :3.000 Median :3.00 Median :4.00
#> Mean :2.255 Mean :2.51 Mean :3.005 Mean :2.91 Mean :3.55
#> 3rd Qu.:3.000 3rd Qu.:3.00 3rd Qu.:4.000 3rd Qu.:4.00 3rd Qu.:5.00
#> Max. :5.000 Max. :5.00 Max. :5.000 Max. :5.00 Max. :5.00
#> x6 x7 x8 x9 x10
#> Min. :1.00 Min. :1.00 Min. :1.000 Min. :1.00 Min. :1.00
#> 1st Qu.:1.00 1st Qu.:1.00 1st Qu.:2.000 1st Qu.:2.00 1st Qu.:1.00
#> Median :2.00 Median :1.00 Median :3.000 Median :3.00 Median :3.00
#> Mean :2.14 Mean :1.82 Mean :2.915 Mean :3.04 Mean :2.59
#> 3rd Qu.:3.00 3rd Qu.:3.00 3rd Qu.:4.000 3rd Qu.:4.00 3rd Qu.:4.00
#> Max. :5.00 Max. :5.00 Max. :5.000 Max. :5.00 Max. :5.00
#> x11 x12
#> Min. :1.000 Min. :1.00
#> 1st Qu.:2.000 1st Qu.:3.00
#> Median :3.000 Median :3.00
#> Mean :2.985 Mean :3.45
#> 3rd Qu.:4.000 3rd Qu.:4.00
#> Max. :5.000 Max. :5.00
# Matrice de corrélation
cormat <- cor(factor, method = "pearson")
corrplot::corrplot(cormat)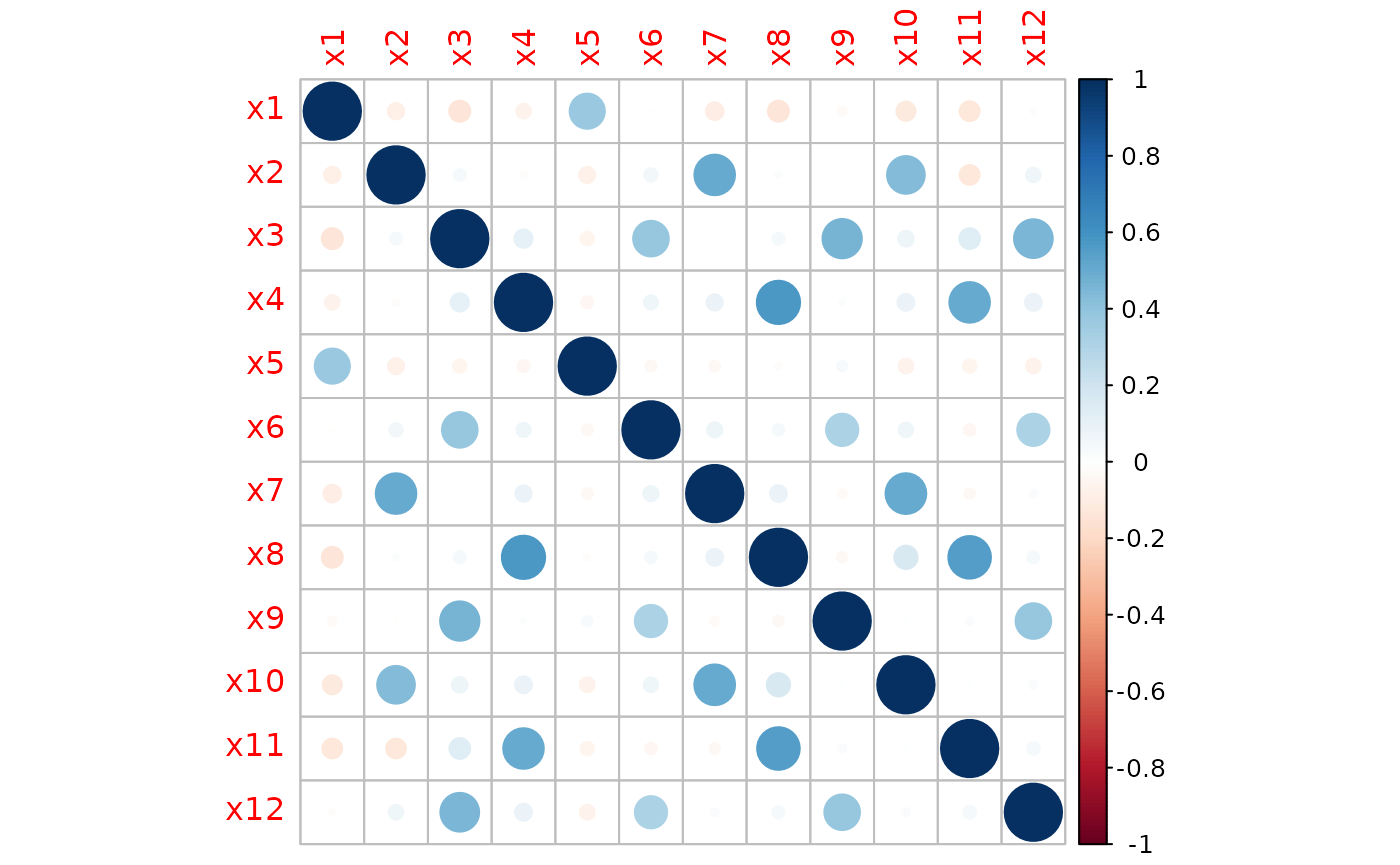
Matrice de corrélation
Estimation
Il y a deux méthodes principales d’estimation:
- la méthode du maximum de vraisemblance, qui suppose que les facteurs et les aléas sont gaussiens et indépendants; cela donne naissance à une fonction de vraisemblance pour la matrice de covariance empirique (Wishart)
- la méthode des composantes principales: on retient uniquement \(k\) vecteurs propres de la matrice de covariance
Dans les deux cas, la solution est identifiable à rotation orthogonale près. Le but de l’analyse factorielle est d’obtenir une solution facilement identifiable: on choisit souvent une rotation varimax, qui tend à donner des chargements qui sont larges ou quasi-nuls.
Estimation par maximum de vraisemblance
La méthode de base dans R consiste à ajuster le
modèle factoriel par maximum de vraisemblance. La fonction
factanal sert à cette tâche, mais le paquet
psych inclut plusieurs autres options.
fa4 <- factanal(x = factor, factors = 4L)
print(fa4$loadings, cutoff = 0.3)
#>
#> Loadings:
#> Factor1 Factor2 Factor3 Factor4
#> x1 0.992
#> x2 0.665
#> x3 0.751
#> x4 0.714
#> x5 0.373
#> x6 0.510
#> x7 0.754
#> x8 0.792
#> x9 0.629
#> x10 0.659
#> x11 0.708
#> x12 0.609
#>
#> Factor1 Factor2 Factor3 Factor4
#> SS loadings 1.673 1.602 1.483 1.153
#> Proportion Var 0.139 0.133 0.124 0.096
#> Cumulative Var 0.139 0.273 0.396 0.493Par défaut, la solution retournée correspond à la rotation varimax. On imprime les chargements en omettant les valeurs inférieures à 0.3 pour faciliter la visualisation.
Puisqu’on ajuste le modèle par maximum de vraisemblance, la sortie inclut un test d’hypothèse que le modèle à \(k\) facteurs pour la matrice de covariance est une simplification adéquate du modèle avec toutes les \(p\) variables originales.
La valeur-p pour le test du rapport de vraisemblance (adéquation de la structure de corrélation paramétrique) basée sur la loi asymptotique khi-carrée est enregistrée dans la liste; avec une valeur-p de 0.97, on a aucune preuve contre l’hypothèse nulle de l’adéquation du modèle de covariance. Une approximation de Bartlett à la statistique du rapport de vraisemblance fournit une meilleure approximation si \(n\) est plus grand que \(p\); ici, la différence est minime avec une valeur-p de 0.98.
fa4$PVAL
# avec correction de Bartlett
bartlettcorr_factanal(fa4)$pvalueLe paquet hecmulti contient des méthodes pour extraire
la log-vraisemblance et les critères d’information pour un modèle
d’analyse factorielle (objet de classe “factanal”). On fait une boucle
pour calculer les AIC, BIC et la valeur-\(p\) du test d’adéquation.
# Tableau avec critères
emv_crit <- ajustement_factanal(
x = factor,
factors = 1:5)
emv_crit
#> k AIC BIC pval npar heywood
#> 1 1 2267.138 2346.297 < 2e-16 24 0
#> 2 2 2137.869 2253.310 < 2e-16 35 0
#> 3 3 2017.188 2165.612 0.09604 45 0
#> 4 4 2002.559 2180.668 0.97262 54 1
#> 5 5 2012.696 2217.192 0.97445 62 1Le nombre de facteurs optimal selon les critères AIC et BIC est trois, et c’est également le nombre minimal de facteurs selon test du khi-deux qui donne une description adéquate de la matrice de covariance.
La variance des aléas (l’unicité, ou uniqueness) est un indicateur de la fiabilité du modèle ajusté par la méthode du maximum de vraisemblance. Une valeur près de 1 (à 0.005) indique que la solution est un cas de Heywood On voit qu’avec quatre ou cinq facteurs, le modèle correspond à un cas de Heywood et la solution est invalide. Cela peut-être dû à plusieurs causes: colinéarité, facteur redondant (avec une corrélation de un avec une des variables), trop grand nombre ou trop petit nombre de facteurs, etc.
Estimation par composantes principales
On peut effectuer une analyse en composantes principales et faire une rotation subséquente des valeurs propres: la décomposition en valeurs propres/vecteurs propres est la même peut importe le nombre de facteurs retenus, le coût est donc moindre à l’autre méthode d’estimation. La solution retournée est également toujours valide si on n’a pas de valeurs manquantes, puisque les corrélations retournées sont positives.
Le choix du nombre de facteurs est moins facile. Deux critères sont employés en pratique: le critère de Kaiser (retenir autant de facteurs qu’il n’y a de valeurs propres de la matrice de corrélation supérieures à 1) et le critère du coude (trouver un nombre de facteurs dans un diagramme d’éboulis à partir duquel le pourcentage de variance exprimée est faible).
On fait la décomposition en valeurs propres/vecteurs propres à la mitaine pour ensuite extraire le nombre de valeurs propres supérieures à 1.
decomposition <- eigen(cov(factor))
valpropres <- decomposition$values
critkaiser <- sum(valpropres > 1)
# Diagramme d'éboulis
eboulis(decomposition)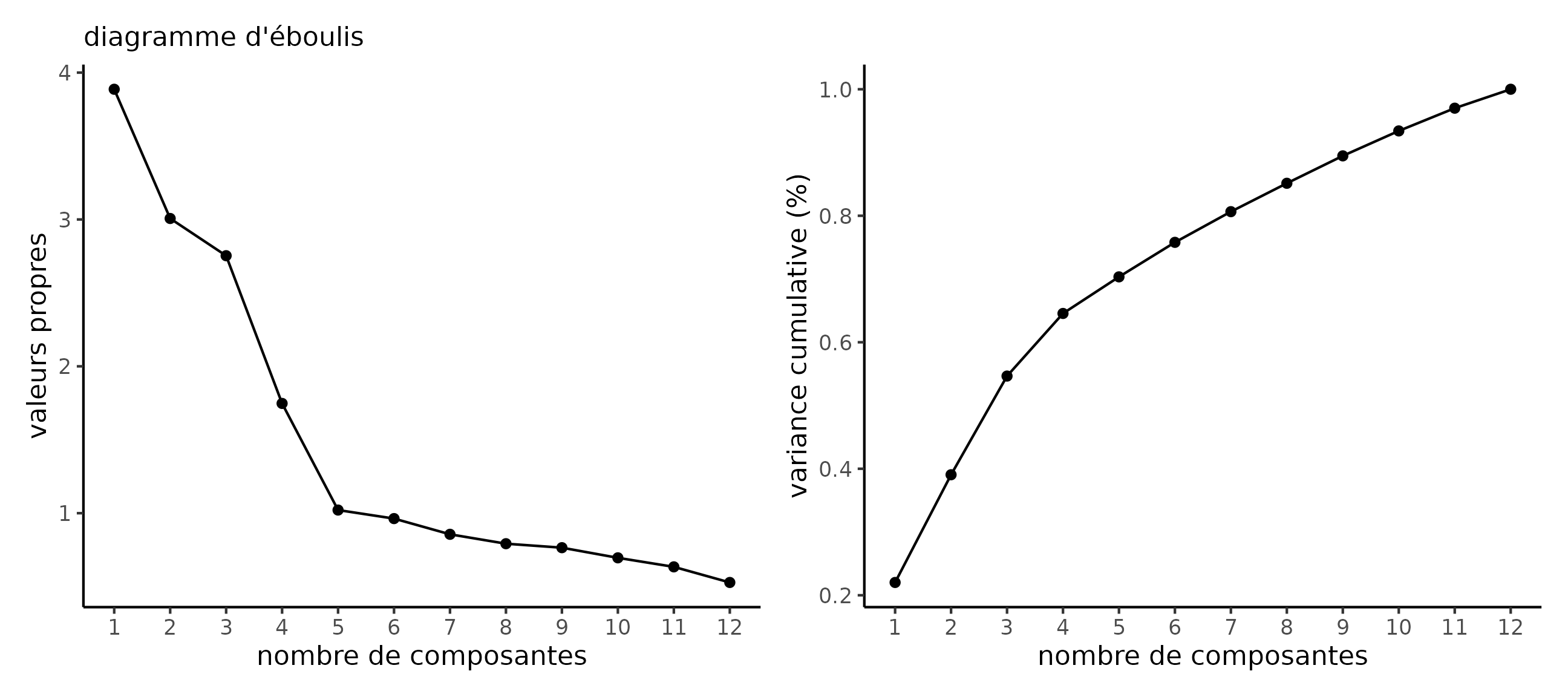
Diagramme d’éboulis
On peut aussi tracer un diagramme d’éboulis, qui suggère cinq facteurs. Si on extrait les cinq premières composantes principales et qu’on effectue une rotation varimax, on recouvre le modèle d’analyse factorielle avec cinq facteurs.
La décomposition en vecteurs propres de la matrice de covariance est \(\boldsymbol{S} = \boldsymbol{Q}\boldsymbol{\Lambda}\boldsymbol{Q}^{-1}\), où \(\boldsymbol{Q}\) est la matrice \(p \times p\) de vecteurs propres et \(\boldsymbol{\Lambda}\) une matrice diagonale contenant les valeurs propres (ordonnées de la plus grande à la plus petite). L’analyse en composantes principales revient à conserver uniquement les \(k\) premières composantes, d’où une racine avec \(\boldsymbol{Q}_{(k)}\boldsymbol{\Lambda}_{(k)}^{1/2}\) où \(\boldsymbol{Q}_{(k)}\) est une matrice \(p \times k\) avec les \(k\) premiers vecteurs propres et \(\boldsymbol{\Lambda}_{k}\) la sous-matrice \(k \times k\) de \(\boldsymbol{\Lambda}\) contenant les \(k\) plus grandes valeurs propres. Il suffit ensuite de calculer la rotation de cette racine.
factocp(factor)
#>
#> Loadings:
#> F2 F1 F3 F4
#> x1 0.812
#> x2 -0.791
#> x3 0.793
#> x4 0.821
#> x5 0.834
#> x6 0.661
#> x7 -0.834
#> x8 0.851
#> x9 0.751
#> x10 -0.787
#> x11 0.818
#> x12 0.731
#>
#> F2 F1 F3 F4
#> SS loadings 2.175 2.116 1.991 1.388
#> Proportion Var 0.181 0.176 0.166 0.116
#> Cumulative Var 0.181 0.358 0.523 0.639La fonction factocp dans hecmulti calcule
directement le modèle, par défaut en utilisant le critère de Kaiser bien
que nfact puisse accommoder un entier représentant le
nombre de facteurs/composantes principales à conserver.
Le paquet psych permet aussi l’estimation (plus directe)
avec d’autres méthodes, notamment la méthode des composantes
principales. Les estimations des chargements devrait être identique à
celle obtenue avec factocp.
Création d’échelles
On calcule simplement les moyennes et on vérifie la cohérence interne. La règle du pouce veut qu’on conserve les échelles si les variables qui les forment ont un \(\alpha\) de Cronbach qui excède 0.6.
ech_service <- rowMeans(factor[,c("x4","x8","x11")])
ech_produit <- rowMeans(factor[,c("x3","x6","x9","x12")])
ech_paiement <- rowMeans(factor[,c("x2","x7","x10")])
ech_prix <- rowMeans(factor[,c("x1","x5")])
# Cohérence interne (alpha de Cronbach)
alphaC(factor[,c("x4","x8","x11")])
#> [1] 0.7805243
alphaC(factor[,c("x3","x6","x9","x12")])
#> [1] 0.7182528
alphaC(factor[,c("x2","x7","x10")])
#> [1] 0.7274919
alphaC(factor[,c("x1","x5")])
#> [1] 0.5456338