Goodness-of-fit plots for parametric models — autoplot.elife

Because of censoring and truncation, the plotting positions must be adjusted accordingly. For right-censored data, the methodology is described in Waller & Turnbull (1992). Only non-censored observations are displayed, which can create distortion.

Usage

autoplot.elife_par(object, ...)

# S3 method for elife_par
plot(
  x,
  plot.type = c("base", "ggplot"),
  which.plot = c("pp", "qq"),
  confint = c("none", "pointwise", "simultaneous"),
  plot = TRUE,
  ...
)

Arguments

object: an object of class elife_par containing the fitted parametric model
...: additional arguments, currently ignored by the function.
x: a parametric model of class elife_par
plot.type: string, one of base for base R or ggplot
which.plot: vector of string indicating the plots, among pp for probability-probability plot, qq for quantile-quantile plot, erp for empirically rescaled plot (only for censored data), exp for standard exponential quantile-quantile plot or tmd for Tukey's mean difference plot, which is a variant of the Q-Q plot in which we map the pair $(x,y)$ is mapped to ((x+y)/2,y-x) are detrended, dens and cdf return the empirical distribution function with the fitted parametric density or distribution function curve superimposed.
confint: logical; if TRUE, creates uncertainty diagnostic via a parametric bootstrap
plot: logical; if TRUE, creates a plot when plot.type="ggplot". Useful for returning ggplot objects without printing the graphs

Value

The function produces graphical goodness-of-fit plots using base R or ggplot objects (returned as an invisible list).

Details

For truncated data, we first estimate the distribution function nonparametrically, $F_n$. The uniform plotting positions of the data $$v_i = [F_n(y_i) - F_n(a_i)]/[F_n(b_i) - F_n(a_i)].$$ For probability-probability plots, the empirical quantiles are transformed using the same transformation, with $F_n$ replaced by the postulated or estimated distribution function $F_0$. For quantile-quantile plots, the plotting positions $v_i$ are mapped back to the data scale viz. $$F_0^{-1}\{F_0(a_i) + v_i[F_0(b_i) - F_0(a_i)]\}$$ When data are truncated and observations are mapped back to the untruncated scale (with, e.g., exp), the plotting positions need not be in the same order as the order statistics of the data.

Examples

set.seed(1234)
samp <- samp_elife(
 n = 200,
 scale = 2,
 shape = 0.3,
 family = "gomp",
 lower = 0, upper = runif(200, 0, 10),
 type2 = "ltrc")
fitted <- fit_elife(
 time = samp$dat,
 thresh = 0,
 event = ifelse(samp$rcens, 0L, 1L),
 type = "right",
 family = "exp",
 export = TRUE)
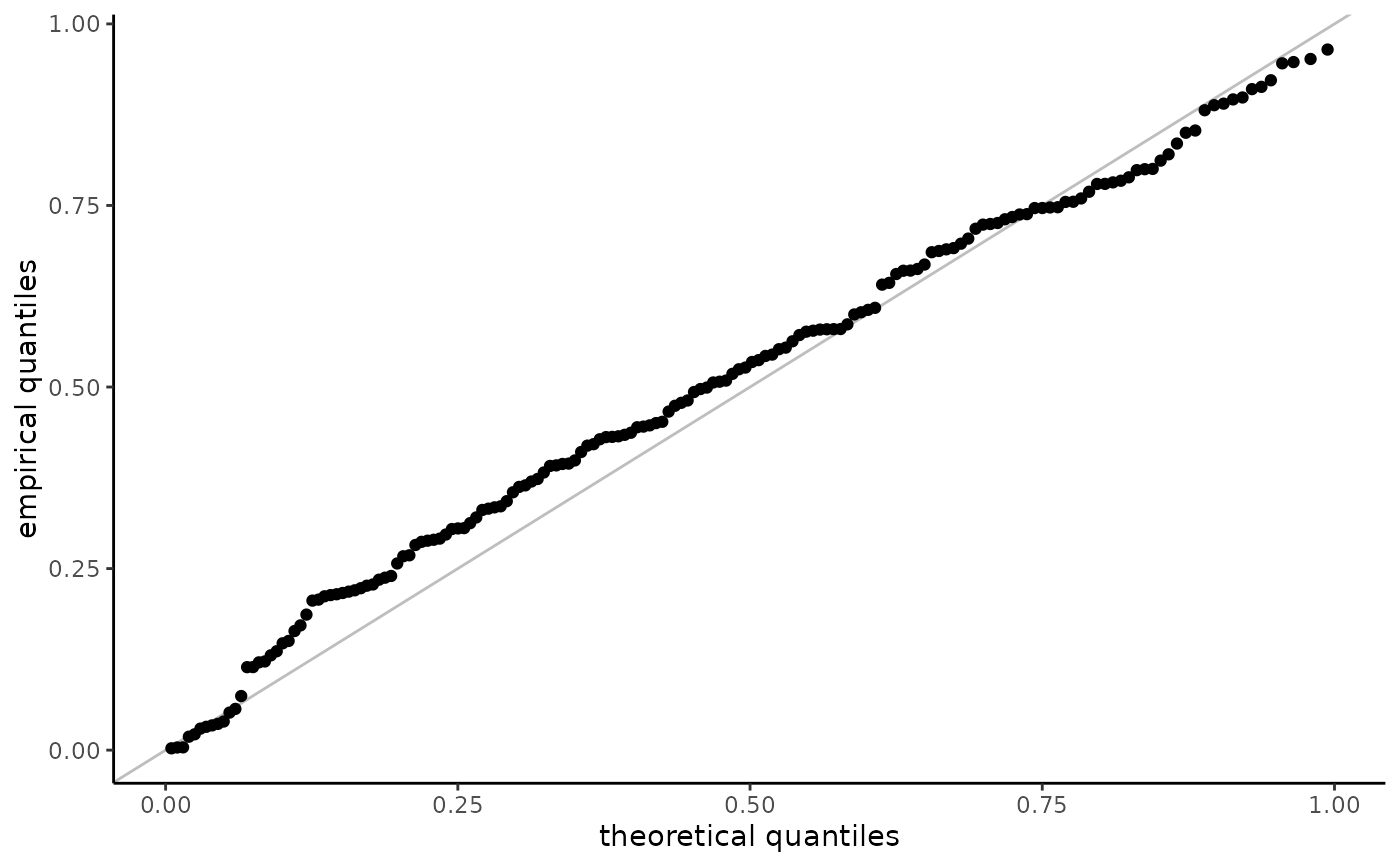
plot(fitted, plot.type = "ggplot")


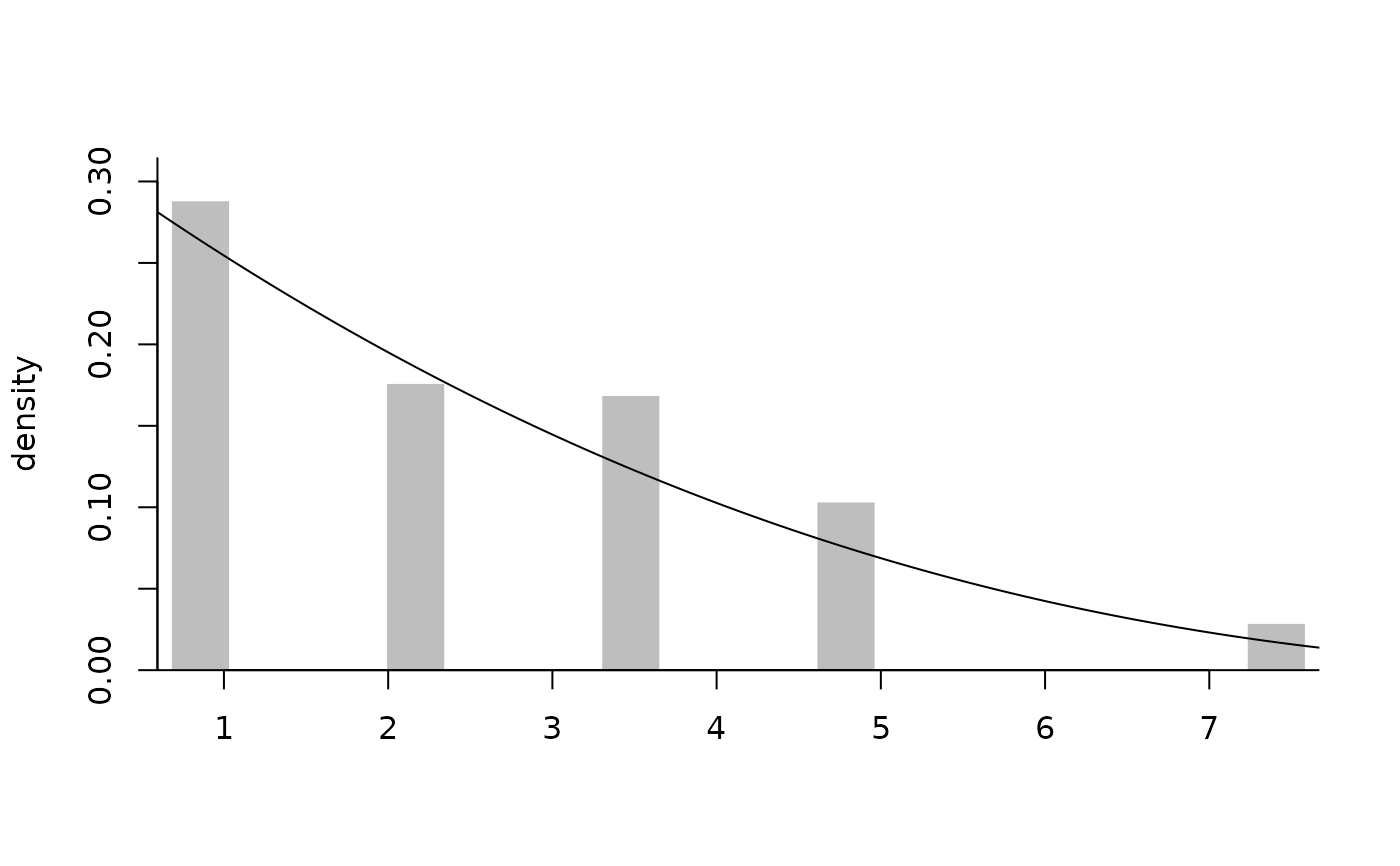
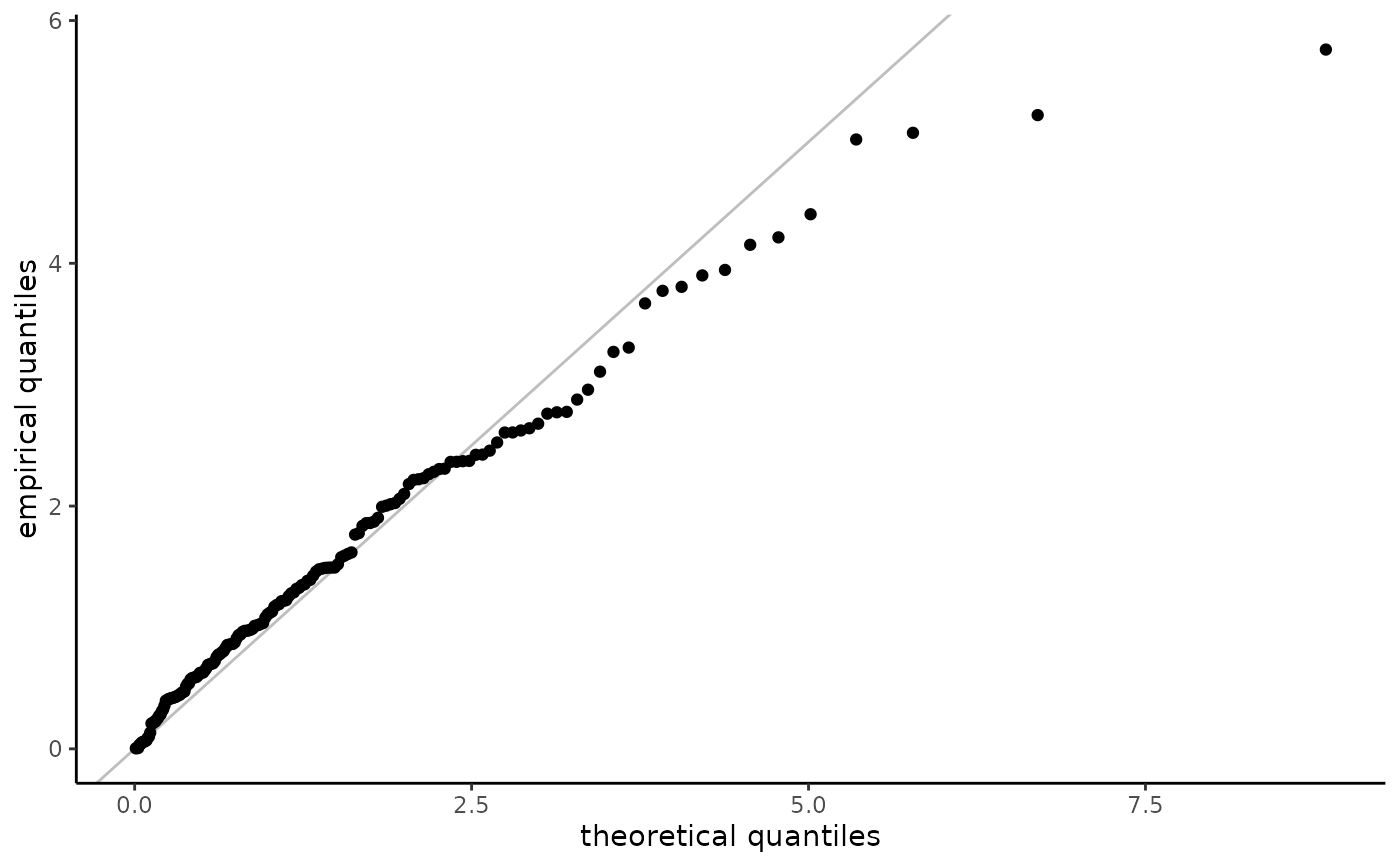# Left- and right-truncated data
n <- 40L
samp <- samp_elife(
 n = n,
 scale = 2,
 shape = 0.3,
 family = "gp",
 lower = ltrunc <- runif(n),
 upper = rtrunc <- ltrunc + runif(n, 0, 15),
 type2 = "ltrt")
fitted <- fit_elife(
 time = samp,
 thresh = 0,
 ltrunc = ltrunc,
 rtrunc = rtrunc,
 family = "gp",
 export = TRUE)
plot(fitted,  which.plot = c("tmd", "dens"))