Introducing longevity

What does longevity do?

The longevity package provides a variety of numerical routines for parametric and nonparametric models for positive data subject to non informative censoring and truncation mechanisms. The package includes functions to estimate various parametric model parameters via maximum likelihood, produce diagnostic plots accounting for survival patterns, compare nested models using analysis of deviance, etc.

The syntax of longevity follows that of the popular survival package, but forgoes the specification of Surv type objects: rather, users must specify some of the following

the time vector time (a left interval if time2 is provided)
the right interval time2 for interval censoring
a vector or scalar event indicating whether data are right, left or interval censored. The option interval2, for interval censoring, is useful if both time and time2 vectors are provided with (potentially zero or infinite bounds) for censored observations.
the status indicator, event, with 0 for right censored, 1 for observed event, 2 for left censored and 3 for interval censored. If omitted, event is set to 1 for all subjects.
ltrunc and rtrunc for left and right truncation values. If omitted, they are set to 0 and \(\infty\), respectively.

The reason for specifying the ltrunc and rtrunc vector outside of the usual arguments is to accomodate instances where there is both interval censoring and interval truncation; survival supports left-truncation right-censoring for time-varying covariate models, but this isn’t really transparent.

Example

We consider Dutch data from CBS; these data were analysed in Einmahl, Einmahl, and Haan (2019). For simplicity, we keep only Dutch people born in the Netherlands, who were at least centenarians when they died and whose death date is known.

thresh0 <- 36525
data(dutch, package = "longevity")
dutch1 <- subset(dutch, ndays > thresh0 & !is.na(ndays) & valid == "A")

We can fit various parametric models accounting for the fact that data are interval truncated. First, we create a list to avoid having to type the name of all arguments repeatedly. These, if not provided directly to function, are selected from the list through arguments.

args <- with(dutch1, list(
  time = ndays,  # time vector
  ltrunc = ltrunc, # left truncation bound
  rtrunc = rtrunc, # right truncation
  thresh = thresh0, # threshold (model only exceedances)
  family = "gp")) # choice of parametric model

The generalized Pareto distribution can be used for extrapolation, provided that the threshold is high enough that shape estimates are more or less stable. To check this, we can produce threshold stability plots, which display point estimates with 95% profile-based pointwise confidence intervals.

tstab_c <- tstab(
  arguments = args,
  family = "gp", # parametric model, here generalized Pareto
  thresh = 102:108 * 365.25, # overwrites thresh
  method = "wald", # type of interval, Wald or profile-likelihood
  plot = FALSE) # by default, calls 'plot' routine
plot(tstab_c, 
     which.plot = "shape", 
     xlab = "threshold (age in days)")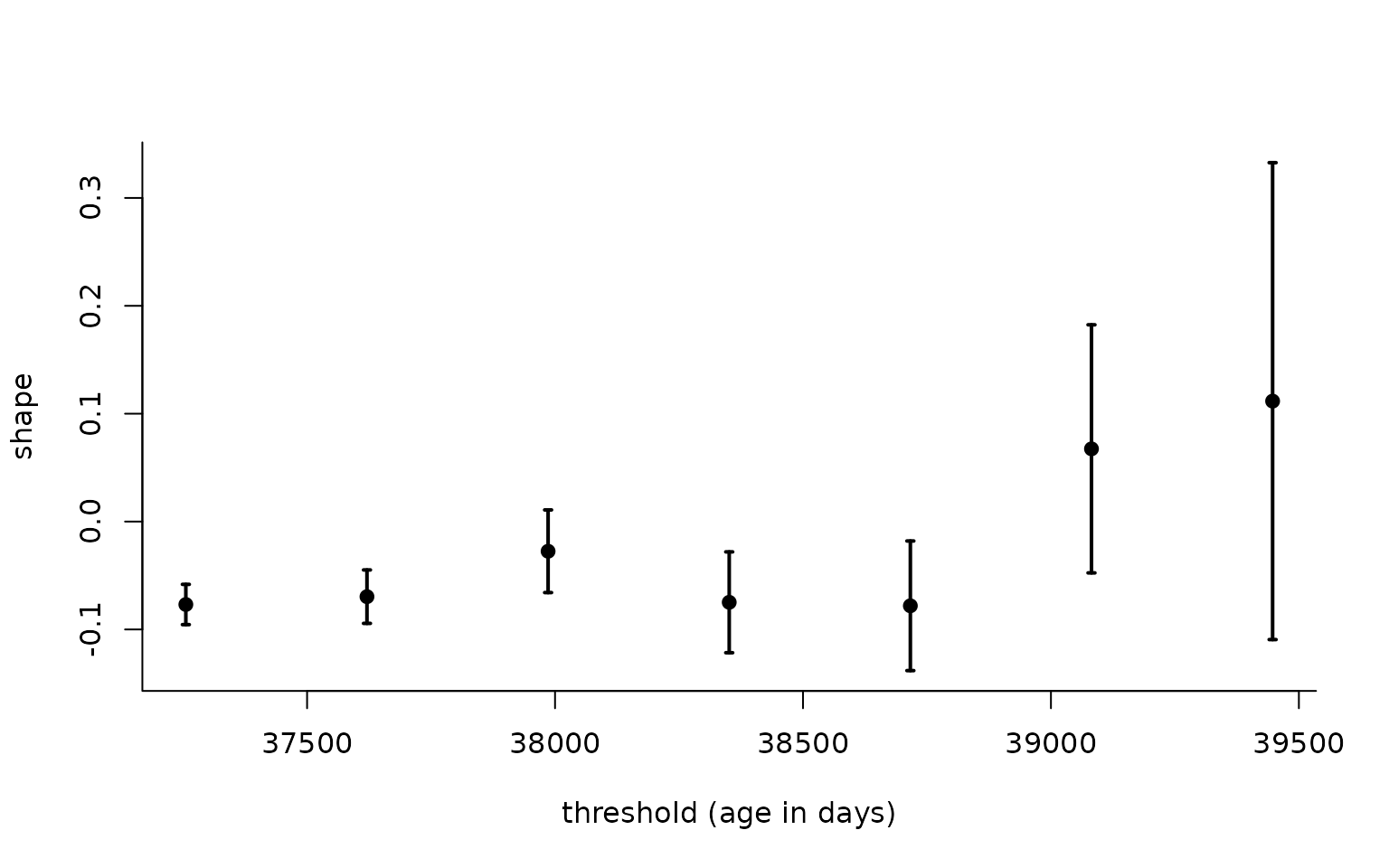

Threshold stability plot with generalized Pareto shape estimates for Dutch data as a function of threshold (in years).

We can fit various parametric models and compare them using the anova call, provided they are nested and share the same data. Diagnostic plots, adapted for survival data, can be used to check goodness-of-fit. These may be computationally intensive to produce in large samples, since they require estimation of the nonparametric maximum likelihood estimator of the distribution function. As such, we pick a relatively high threshold, 108 years, to reduce the computational burden.

(m1 <- fit_elife(arguments = args, 
          thresh = 108 * 365.25,
          family = "gp",
          export = TRUE))

## Model: generalized Pareto distribution. 
## Sampling: interval truncated
## Log-likelihood: -631.242 
## 
## Threshold: 39447 
## Number of exceedances: 90 
## 
## Estimates
##   scale    shape  
## 412.688    0.112  
## 
## Standard Errors
## scale  shape  
## 1.414  0.113  
## 
## Optimization Information
##   Convergence: TRUE

m0 <- fit_elife(arguments = args, 
          thresh = 108 * 365.25,
          family = "exp")
anova(m1, m0)

##     npar Deviance Df     Chisq Pr(>Chisq)
## gp     2 1262.483 NA        NA         NA
## exp    1 1263.112  1 0.6287453  0.4278159

plot(m1, which.plot = "qq")

Quantile-quantile plot of generalized Pareto model to exceedances above 108 years for Dutch.

References

Einmahl, Jesson J., John H. J. Einmahl, and Laurens de Haan. 2019. “Limits to Human Life Span Through Extreme Value Theory.” Journal of the American Statistical Association 114 (527): 1075–80. https://doi.org/10.1080/01621459.2018.1537912.

Léo Belzile

2024-07-05

What does longevity do?

Example

References