Ce chapitre couvre des rappels mathématiques de probabilité et statistique d’ordinaire couverts dans un cours de niveau collégial ou préuniversitaire.
Ce qui différencie la statistique des autres sciences est la prise en compte de l’incertitude et de la notion d’aléatoire. Règle générale, on cherche à estimer une caractéristique d’une population définie à l’aide d’un échantillon (un sous-groupe de la population) de taille restreinte.
La population d’intérêt est un ensemble d’individus formant la matière première d’une étude statistique. Par exemple, pour l’Enquête sur la population active (EPA) de Statistique Canada, « la population cible comprend la population canadienne civile non institutionnalisée de 15 ans et plus ». Même si on faisait un recensement et qu’on interrogeait tous les membres de la population cible, la caractéristique d’intérêt peut varier selon le moment de la collecte; une personne peut trouver un emploi, quitter le marché du travail ou encore se retrouver au chômage. Cela explique la variabilité intrinsèque.
En général, on se base sur un échantillon pour obtenir de l’information parce que l’acquisition de données est coûteuse. L’inférence statistique vise à tirer des conclusions, pour toute la population, en utilisant seulement l’information contenue dans l’échantillon et en tenant compte des sources de variabilité. Le sondeur George Gallup (traduction libre) a fait cette merveilleuse analogie entre échantillon et population:
«Il n’est pas nécessaire de manger un bol complet de soupe pour savoir si elle est trop salé; pour autant qu’elle ait été bien brassée, une cuillère suffit.»
Un échantillon est un sous-groupe d’individus de la population. Si on veut que ce dernier soit représentatif, il devrait être tiré aléatoirement de la population, ce qui nécessite une certaine connaissance de cette dernière. Au siècle dernier, les bottins téléphoniques pouvaient servir à créer des plans d’enquête. C’est un sujet complexe et des cours entiers d’échantillonnage y sont consacrés. Même si on ne collectera pas de données, il convient de noter la condition essentielle pour pouvoir tirer des conclusions fiables à partir d’un échantillon: ce dernier doit être représentatif de la population étudiée, en ce sens que sa composition doit être similaire à celle de la population, et aléatoire. On doit ainsi éviter les biais de sélection, notamment les échantillons de commodité qui consistent en une sélection d’amis et de connaissances.
Si notre échantillon est aléatoire, notre mesure d’une caractéristique d’intérêt le sera également et la conclusion de notre procédure de test variera d’un échantillon à l’autre. Plus la taille de ce dernier est grande, plus on obtiendra une mesure précise de la quantité d’intérêt. L’exemple suivant illustre pourquoi le choix de l’échantillon est important.
Exemple 1.1 (Gallup et l’élection présidentielle américaine de 1936) Désireuse de prédire le résultat de l’élection présidentielle américaine de 1936, la revue Literary Digest a sondé 10 millions d’électeurs par la poste, dont 2.4 millions ont répondu au sondage en donnant une nette avance au candidat républicain Alf Landon (57%) face au président sortant Franklin D. Roosevelt (43%). Ce dernier a néanmoins remporté l’élection avec 62% des suffrages, une erreur de prédiction de 19%. Le plan d’échantillonnage avait été conçu en utilisant des bottins téléphoniques, des enregistrements d’automobiles et des listes de membres de clubs privés, etc.: la non-réponse différentielle et un échantillon biaisé vers les classes supérieures sont en grande partie responsable de cette erreur.
Gallup avait de son côté correctement prédit la victoire de Roosevelt en utilisant un échantillon aléatoire de (seulement) 50 000 électeurs. Vous pouvez lire l’histoire complète (en anglais).
Le résultat d’une collecte de données est un tableau, ou base de données, contenant sur chaque ligne des observations et en colonne des variables. Le Tableau 1.1 donne un exemple de structure.
renfe, qui contient les prix de 10K billets de train entre Barcelone et Madrid. Les colonnes prix et duree sont des variables numériques continues, les autres des variables catégorielles.
| prix | type | classe | tarif | dest | duree | jour |
|---|---|---|---|---|---|---|
| 143.4 | AVE | Preferente | Promo | Barcelone-Madrid | 190 | 6 |
| 181.5 | AVE | Preferente | Flexible | Barcelone-Madrid | 190 | 2 |
| 86.8 | AVE | Preferente | Promo | Barcelone-Madrid | 165 | 7 |
| 86.8 | AVE | Preferente | Promo | Barcelone-Madrid | 190 | 7 |
| 69.0 | AVE-TGV | Preferente | Promo | Barcelone-Madrid | 175 | 4 |
Le choix de modèle statistique ou de test dépend souvent du type de variables collectées. Les variables peuvent être de plusieurs types: quantitatives (discrètes ou continues) si elles prennent des valeurs numériques, qualitatives (binaires, nominales ou ordinales) si elles peuvent être décrites par un adjectif; je préfère le terme catégorielle, plus évocateur.
La plupart des modèles avec lesquels nous interagirons sont des modèles dits de régression, dans lesquelles on modélisation la moyenne d’une variable quantitative en fonction d’autres variables dites explicatives. Il y a deux types de variables numériques:
Les variables catégorielles représentent un ensemble fini de possibilités. On les regroupe en deux types, pour lesquels on ne fera pas de distinction:
La codification des modalités des variables catégorielle est arbitraire; en revanche, on préservera l’ordre lorsqu’on représentera graphiquement les variables ordinales. Lors de l’estimation, chaque variable catégorielle doit est transformée en un ensemble d’indicateurs binaires 0/1: il est donc essentiel de déclarer ces dernières dans votre logiciel statistique, surtout si elles sont parfois encodées dans la base de données à l’aide de valeurs entières.
Suppsons qu’on cherche à décrire le comportement d’un phénomène aléatoire. Pour ce faire, on cherche à décrire l’ensemble des valeurs possibles et leur probabilité/fréquence relative au sein de la population: ces dernières sont encodées dans la loi de la variable aléatoire.
On dénote les variables aléatoires par des lettres majuscules, et leurs réalisations par des minuscules: par exemple, \(Y \sim \mathsf{normale}(\mu, \sigma^2)\) indique que \(Y\) suit une loi normale de paramètres \(\mu \in \mathbb{R}\) et \(\sigma > 0\). On parle de famille de lois si la valeur des paramètres ne sont pas spécifiées; si on fixe plutôt ces dernière, on obtient une représentation qui encode les probabilité.
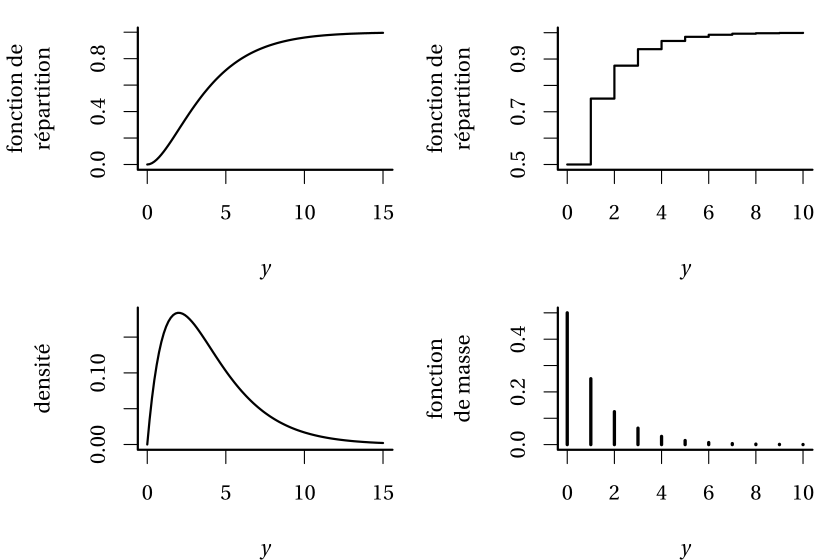
Définition 1.1 (Fonctions de répartition, de masse et de densité) La fonction de répartition \(F(y)\) donne la probabilité cumulative qu’un événement n’excède pas une variable donnée, \(F(y) = \mathsf{Pr}(Y \leq y)\). Si la variable \(Y\) prend des valeurs discrètes, alors on utilise la fonction de masse \(f(y)=\mathsf{Pr}(Y=y)\) qui donne la probabilité pour chacune des valeurs de \(y\). Si la variable \(Y\) est continue, aucune valeur numérique de \(y\) n’a de probabilité non-nulle et \(\Pr(Y=y) = 0\) pour toute valeur réelle \(y\); la densité, aussi dénotée \(f(x)\), est une fonction est non-négative et satisfait \(\int_{\mathbb{R}} f(x) \mathrm{d}x=1\): elle décrit la probabilité d’obtenir un résultat dans un ensemble donné des réels \(\mathbb{R}\), pour n’importe lequel intervalle. La densité sert à estimer la probabilité que la variable continue \(Y\) appartienne à un ensemble \(B\), via \(\mathsf{Pr}(Y \in B) = \int_B f(y) \mathrm{d} y\); la fonction de répartition est ainsi définie comme \(F(y) = \int_{-\infty}^y f(x) \mathrm{d} x\).
Un premier cours de statistique débute souvent par la présentation de statistiques descriptives comme la moyenne et l’écart-type. Ce sont des estimateurs des moments (centrés), qui caractérisent la loi du phénomène d’intérêt. Dans le cas de la loi normale unidimensionnelle, qui a deux paramètres, l’espérance et la variance caractérisent complètement le modèle.
Définition 1.2 (Moments) Soit \(Y\) une variable aléatoire de fonction de densité (ou de masse) \(f(x)\). On définit l’espérance d’une variable aléatoire \(Y\) comme \[\begin{align*} \mathsf{E}(Y)=\int_{\mathbb{R}} y f(y) \mathrm{d} y. \end{align*}\] L’espérance est la « moyenne théorique», ou moment de premier ordre : dans le cas discret, \(\mu = \mathsf{E}(Y)=\sum_{y \in \mathcal{y}} y \mathsf{Pr}(y=y)\), où \(\mathcal{Y}\) représente le support de la loi, à savoir les valeurs qui peuvent prendre \(Y\). Plus généralement, l’espérance d’une fonction \(g(y)\) pour une variable aléatoire \(Y\) est simplement l’intégrale de \(g(y)\) pondérée par la densité \(f(y)\). De même, si l’intégrale est convergente, la variance est \[\begin{align*} \mathsf{Va}(Y)&=\int_{\mathbb{R}} (y-\mu)^2 f(y) \mathrm{d} y \\&=\mathsf{E}\{Y-\mathsf{E}(Y)\}^2 \\&= \mathsf{E}(Y^2) - \{\mathsf{E}(Y)\}^2. \end{align*}\]
L’écart-type est défini comme la racine carrée de la variance, \(\mathsf{sd}(Y)=\sqrt{\mathsf{Va}(Y)}\): elle est exprimé dans les mêmes unités que celle de \(Y\) et donc plus facilement interprétable.
Exemple 1.2 Considérons une variable aléatoire discrète \(Y\) pour la somme de deux lancers de dés à six faces. L’espérance de \(g(Y)=Y^2\) est \[\begin{align*} \mathsf{E}(Y^2) &= (2^2 + 12^2) \times \frac{1}{36} + (3^2 + 11^2) \times \frac{2}{36} + (4^2 + 10^2) \\&\;\times \frac{3}{36} + (5^2 +9^2) \times \frac{4}{36} + (6^2 + 8^2) \times \frac{5}{36} \\& + 7^2 \times \frac{6}{36}= \frac{329}{6}. \end{align*}\]
La notion de moments peut être généralisé à des vecteurs. Si \(\boldsymbol{Y}\) est un \(n\)-vecteur, comprenant par exemple dans le cadre d’une régression des mesures d’un ensemble d’observations, alors l’espérance est calculée composante par composante,
\[\begin{align*} \mathsf{E}(\boldsymbol{Y}) &= \boldsymbol{\mu}= \begin{pmatrix} \mathsf{E}(Y_1) & \cdots & \mathsf{E}(Y_n) \end{pmatrix}^\top \end{align*}\] tandis que la matrice \(n \times n\) de deuxième moments centrés de \(\boldsymbol{Y}\), dite matrice de variance ou matrice de covariance, est \[\begin{align*} \mathsf{Va}(\boldsymbol{Y}) &= \boldsymbol{\Sigma} = \begin{pmatrix} \mathsf{Va}(Y_1) & \mathsf{Co}(Y_1, Y_2) & \cdots & \mathsf{Co}(Y_1, Y_n) \\ \mathsf{Co}(Y_2, Y_1) & \mathsf{Va}(Y_2) & \ddots & \vdots \\ \vdots & \ddots & \ddots & \vdots \\ \mathsf{Co}(Y_n, Y_1) & \mathsf{Co}(Y_n, Y_2) &\cdots & \mathsf{Va}(Y_n) \end{pmatrix} \end{align*}\] Le \(i\)e élément diagonal de \(\boldsymbol{\Sigma}\), \(\sigma_{ii}=\sigma_i^2\), est la variance de \(Y_i\), tandis que les éléments hors de la diagonale, \(\sigma_{ij}=\sigma_{ji}\) \((i \neq j)\), sont les covariances des paires \[\begin{align*} \mathsf{Co}(Y_i, Y_j) = \int_{\mathbb{R}^2} (y_i-\mu_i)(y_j-\mu_j) f_{Y_i, Y_j}(y_i, y_j) \mathrm{d} y_i \mathrm{d} y_j. \end{align*}\] Par construction, la matrice de covariance \(\boldsymbol{\Sigma}\) est symmétrique. Il est d’usage de considérer la relation deux-à-deux de variables standardisées, afin de séparer la dépendance linéaire de la variabilité de chaque composante. La corrélation linéaire entre \(Y_i\) et \(Y_j\) est \[\begin{align*} \rho_{ij}=\mathsf{Cor}(Y_i,Y_j)=\frac{\mathsf{Co}(Y_i, Y_j)}{\sqrt{\mathsf{Va}(Y_i)}\sqrt{\mathsf{Va}(Y_j)}}=\frac{\sigma_{ij}}{\sigma_i\sigma_j}. \end{align*}\] La matrice de corrélation de \(\boldsymbol{Y}\) est une matrice symmétrique \(n\times n\) avec des uns sur la diagonale et les corrélations des pairs hors diagonale, \[\begin{align*} \mathsf{Cor}(\boldsymbol{Y})= \begin{pmatrix} 1 & \rho_{12} & \rho_{13} & \cdots & \rho_{1n}\\ \rho_{21} & 1 & \rho_{23} & \cdots & \rho_{2n} \\ \rho_{31} & \rho_{32} & 1 & \ddots & \rho_{3n} \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ \rho_{n1} & \rho_{n2} & \rho_{n3} & \cdots & 1 \end{pmatrix}. \end{align*}\] Nous modéliserons la matrice de covariance ou de corrélation des données corrélées et longitudinales par individus du même groupe (ou du même individu pour les mesures répétées) dans le Chapitre 5.
Définition 1.3 (Corrélation linéaire de Pearson) Le coefficient de corrélation linéaire entre \(X_j\) et \(X_k\), que l’on note \(r_{j, k}\), cherche à mesurer la force de la relation linéaire entre deux variables, c’est-à-dire à quantifier à quel point les observations sont alignées autour d’une droite. Le coefficient de corrélation est \[\begin{align*} r_{j, k} &= \frac{\widehat{\mathsf{Co}}(X_j, X_k)}{\{\widehat{\mathsf{Va}}(X_j) \widehat{\mathsf{Va}}(X_k)\}^{1/2}} %\\&=\frac{\sum_{i=1}^n (x_{i, j}-\overline{x}_j)(x_{i, k} -\overline{x}_{k})}{\left\{\sum_{i=1}^n (x_{i, j}-\overline{x}_j)^2 \sum_{i=1}^n(x_{i, k} -\overline{x}_{k})^2\right\}^{1/2}} \end{align*}\]
Les propriétés les plus importantes du coefficient de corrélation linéaire \(r\) sont les suivantes:
Règle générale,
La Figure 1.2 montre bien ce dernier point: ces jeux de données ont la même corrélation linéaire (quasi-nulle) et donc la même droite de régression, mais ne sont clairement pas indépendantes puisqu’elles permettent de dessiner un dinosaure ou une étoile.
datasauRus, avec une corrélation linéaire de -0.06 et des statistiques descriptives moyenne, écart-type, etc. identiques pour chaque jeu de données.
Définition 1.4 (Biais) Le biais d’un estimateur \(\hat{\theta}\) pour un paramètre \(\theta\) est \[\begin{align*} \mathsf{biais}(\hat{\theta})=\mathsf{E}(\hat{\theta})- \theta \end{align*}\] L’estimateur est non biaisé si \(\mathsf{biais}(\hat{\theta})=0\).
Exemple 1.3 (Estimateurs sans biais) L’estimateur sans biais de l’espérance de \(Y\) pour un échantillon aléatoire simple \(Y_1, \ldots, Y_n\) est la moyenne empirique \(\overline{Y}_n = n^{-1} \sum_{i=1}^n Y_i\) et celui de la variance \(S_n = (n-1)^{-1} \sum_{i=1}^n (Y_i-\overline{Y})^2\).
Un estimateur sans biais est souhaitable, mais pas toujours optimal. Quelquefois, il n’existe pas d’estimateur non-biaisé pour un paramètre! Dans plusieurs cas, on cherche un estimateur qui minimise l’erreur quadratique moyenne.
Souvent, on cherche à balancer le biais et la variance: rappelez-vous qu’un estimateur est une variable aléatoire (étant une fonction de variables aléatoires) et qu’il est lui-même variable: même s’il est sans biais, la valeur numérique obtenue fluctuera d’un échantillon à l’autre.
Définition 1.5 (Erreur quadratique moyenne) On peut chercher un estimateur qui minimise l’erreur quadratique moyenne, \[\begin{align*} \mathsf{EQM}(\hat{\theta}) = \mathsf{E}\{(\hat{\theta}-\theta)^2\}=\mathsf{Va}(\hat{\theta}) + \{\mathsf{E}(\hat{\theta})\}^2. \end{align*}\] Cette fonction objective est donc un compromis entre le carré du biais et la variance de l’estimateur.
La plupart des estimateurs que nous considérerons dans le cadre du cours sont des estimateurs du maximum de vraisemblance. Ces derniers sont asymptotiquement efficaces, c’est-à-dire qu’ils minimisent l’erreur quadratique moyenne parmi tous les estimateurs possibles quand la taille de l’échantillon est suffisamment grande. Ils ont également d’autre propriétés qui les rendent attractifs comme choix par défaut pour l’estimation. Il ne sont pas nécessairement sans biais
Plusieurs lois aléatoires décrivent des phénomènes physiques simples et ont donc une justification empirique; on revisite les distributions ou loi discrètes les plus fréquemment couvertes.
Définition 1.6 (Loi de Bernoulli) On considère un phénomène binaire, comme le lancer d’une pièce de monnaie (pile/face). De manière générale, on associe les deux possibilités à succès/échec et on suppose que la probabilité de “succès” est \(p\). Par convention, on représente les échecs (non) par des zéros et les réussites (oui) par des uns. Donc, si la variable \(Y\) vaut \(0\) ou \(1\), alors \(\mathsf{Pr}(Y=1)=p\) et la probabilité complémentaire est \(\mathsf{Pr}(Y=0)=1-p\). La fonction de masse de la loi Bernoulli s’écrit de façon plus compacte \[\begin{align*} \mathsf{Pr}(Y=y) = p^y (1-p)^{1-y}, \quad y=0, 1. \end{align*}\]
Un calcul rapide montre que \(\mathsf{E}(Y)=p\) et \(\mathsf{Va}(Y)=p(1-p)\). Effectivement, \[\begin{align*} \mathsf{E}(Y) = \mathsf{E}(Y^2) = p \cdot 1 + (1-p) \cdot 0 = p. \end{align*}\]
Voici quelques exemples de questions de recherches comprenant une variable réponse binaire:
Plus généralement, on aura accès à des données aggrégées.
Exemple 1.4 (Loi binomiale) Si les données représentent la somme d’événements Bernoulli indépendants, la loi du nombre de réussites \(Y\) pour un nombre d’essais donné \(m\) est dite binomiale, dénotée \(\mathsf{Bin}(m, p)\); sa fonction de masse est \[\begin{align*} \mathsf{Pr}(Y=y) = \binom{m}{y}p^y (1-p)^{m-y}, \quad y=0, 1, \ldots, m. \end{align*}\] La vraisemblance pour un échantillon de la loi binomiale est (à constante de normalisation près qui ne dépend pas de \(p\)) la même que pour un échantillon aléatoire de \(m\) variables Bernoulli indépendantes. L’espérance d’une variable binomiale est \(\mathsf{E}(Y)=mp\) et la variance \(\mathsf{Va}(Y)=mp(1-p)\).
On peut ainsi considérer le nombre de personnes qui ont obtenu leur permis de conduire parmi \(m\) candidat(e)s ou le nombre de clients sur \(m\) qui ont passé une commande de plus de 10$ dans un magasin.
Plus généralement, on peut considérer des variables de dénombrement qui prennent des valeurs entières. Parmi les exemples de questions de recherches comprenant une variable réponse de dénombrement:
Exemple 1.5 (Loi de Poisson) Si la probabilité d’un événement Bernoulli est petite et qu’il est rare d’obtenir un succès dans le sens où \(mp \to \lambda\) quand le nombre d’essais \(m\) augmente, alors le nombre de succès suit approximateivement une loi de Poisson de fonction de masse \[\begin{align*} \mathsf{Pr}(Y=y) = \frac{\exp(-\lambda)\lambda^y}{\Gamma(y+1)}, \quad y=0, 1, 2, \ldots \end{align*}\] où \(\Gamma(\cdot)\) dénote la fonction gamma, et \(\Gamma(y+1) = y!\) si \(y\) est un entier. Le paramètre \(\lambda\) de la loi de Poisson représente à la fois l’espérance et la variance de la variable, c’est-à-dire que \(\mathsf{E}(Y)=\mathsf{Va}(Y)=\lambda\).
Exemple 1.6 (Loi binomiale négative) On considère une série d’essais Bernoulli de probabilité de succès \(p\) jusqu’à l’obtention de \(m\) succès. Soit \(Y\), le nombre d’échecs: puisque la dernière réalisation doit forcément être un succès, mais que l’ordre des succès/échecs précédents n’importe pas, la fonction de masse de la loi binomiale négative est \[\begin{align*} \mathsf{Pr}(Y=y)= \binom{m-1+y}{y} p^m (1-p)^{y}. \end{align*}\]
La loi binomiale négative apparaît également si on considère la loi non-conditionnelle du modèle hiérarchique gamma-Poisson, dans lequel on suppose que le paramètre de la moyenne de la loi Poisson est aussi aléatoire, c’est-à-dire \(Y \mid \Lambda=\lambda \sim \mathsf{Po}(\lambda)\) et \(\Lambda\) suit une loi gamma de paramètre de forme \(r\) et de paramètre d’échelle \(\theta\), dont la densité est \[\begin{align*} f(x) = \theta^{-r}x^{r-1}\exp(-x/\theta)/\Gamma(r).\end{align*}\] Le nombre d’événements suit alors une loi binomiale négative.
La paramétrisation la plus courante pour la modélisation est légèrement différente: pour un paramètre \(r>0\) (pas forcément entier), on écrit la fonction de masse \[\begin{align*} \mathsf{Pr}(Y=y)=\frac{\Gamma(y+r)}{\Gamma(y+1)\Gamma(r)} \left(\frac{r}{r + \mu} \right)^{r} \left(\frac{\mu}{r+\mu}\right)^y, \end{align*}\] où \(\Gamma\) dénote la fonction gamma. Dans cette paramétrisation, la moyenne théorique et la variance sont \(\mathsf{E}(Y)=\mu\) et \(\mathsf{Va}(Y)=\mu+k\mu^2\), où \(k=1/r\). La variance d’une variable binomiale négative est supérieure à sa moyenne et le modèle est utilisé comme alternative à la loi de Poisson pour modéliser la surdispersion.
On considère plusieurs lois de variables aléatoires continues; certaines servent de lois pour des tests d’hypothèse et découlent du théorème central limite (notamment les lois normales, Student, Fisher ou \(F\), et khi-deux).
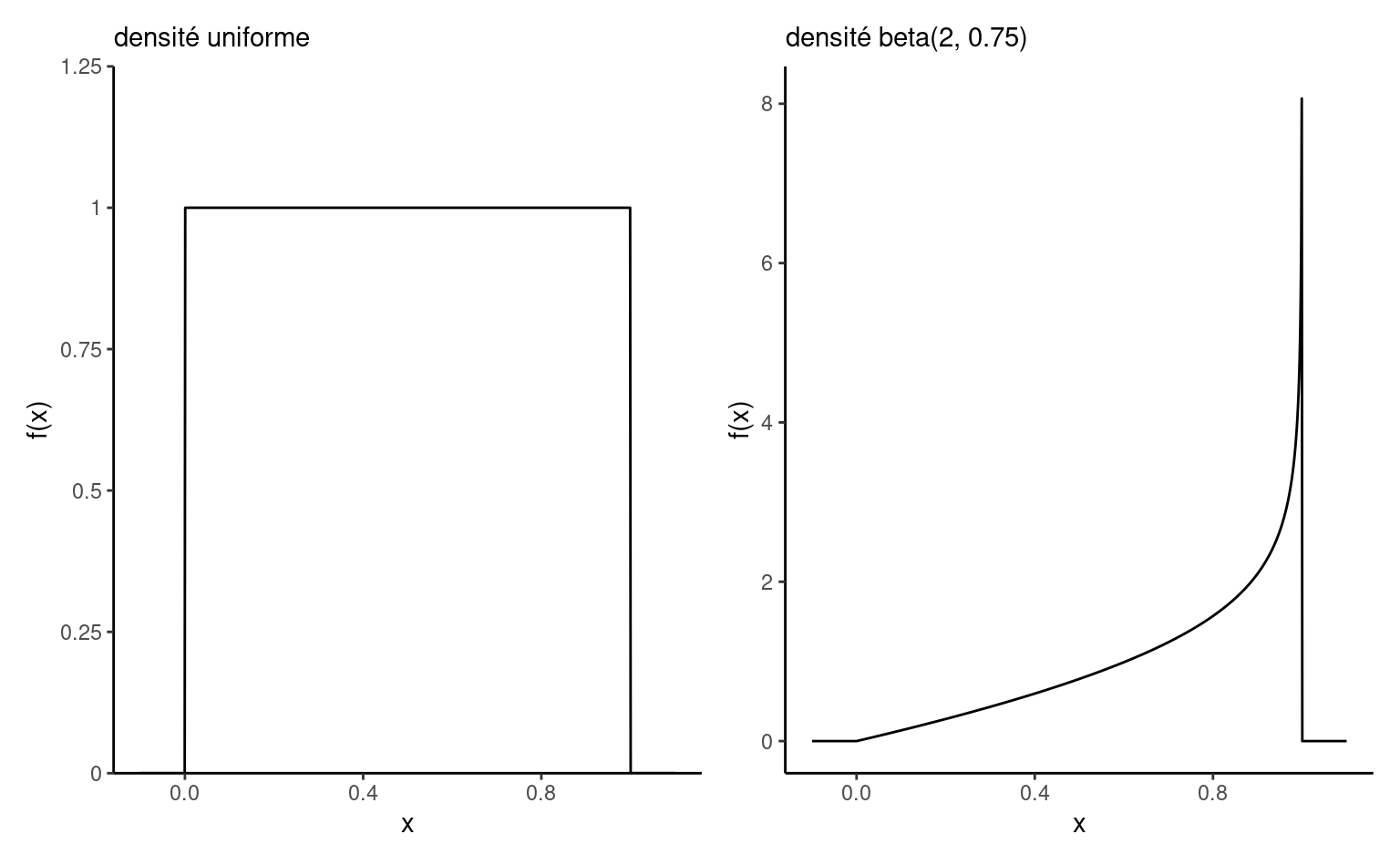
Définition 1.7 (Loi beta) La loi beta \(\mathsf{Beta}(\alpha, \beta)\) est une loi sur l’intervalle \([0,1]\) avec paramètres de forme \(\alpha>0\) et \(\beta>0\). Sa densité est \[\begin{align*} f(x) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}x^{\alpha-1}(1-x)^{1-\beta}, \qquad x \in [0,1]. \end{align*}\] Le cas \(\alpha=\beta=1\), dénotée également \(\mathsf{unif}(0,1)\), correspond à la loi standard uniforme.
Définition 1.8 (Loi exponentielle) La loi exponentielle figure de manière proéminente dans l’étude des temps d’attente pour les phénomènes Poisson et en analyse de survie. Une caractéristique clé de la loi est son absence de mémoire: \(\Pr(Y \geq y + u \mid Y > u) = \Pr(Y > u)\) pour \(Y > 0\) et \(y, u>0\).
La fonction de répartition de la loi exponentielle \(Y \sim \mathsf{Exp}(\beta)\) où \(\beta>0\), est \(F(x) = 1-\exp(-\beta x)\) et sa fonction de densité est \(f(x) =\beta\exp(-\beta x)\) pour \(x >0\). La moyenne théorique de la loi est \(\beta\).
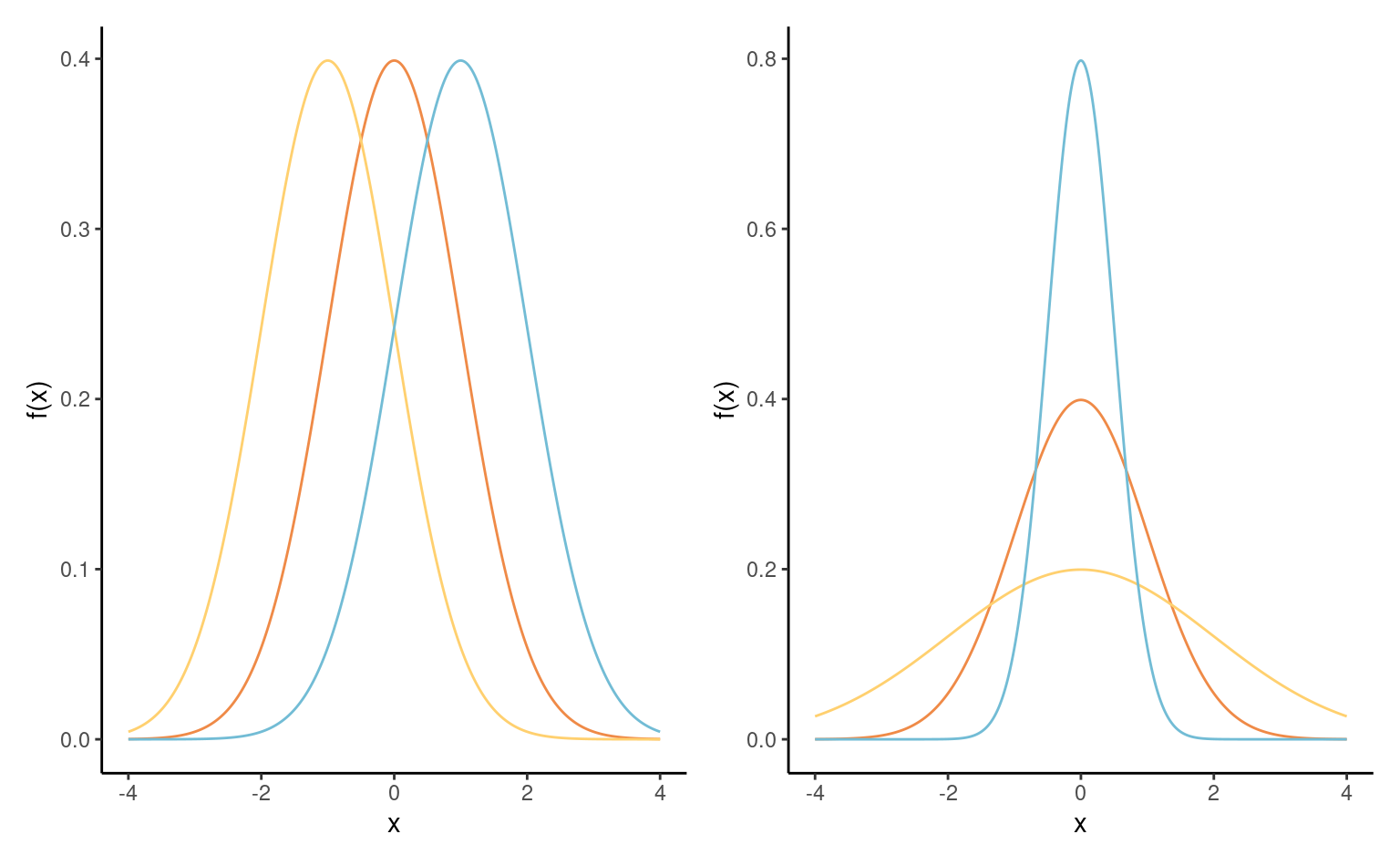
Définition 1.9 (Loi normale) De loin la plus continue des distributions, la loi normale intervient dans le théorème central limite, qui dicte le comportement aléatoire de la moyenne de grand échantillons. La loi normale est pleinement caractérisée par son espérance \(\mu \in \mathbb{R}\) et son écart-type \(\sigma>0\). Loi symmétrique autour de \(\mu\), c’est une famille de localisation et d’échelle. Sa fonction de densité, \[\begin{align*} f(x) = (2\pi\sigma^2)^{-1/2} \exp \left\{ - \frac{(x-\mu)^2}{2\sigma^2}\right\}, \qquad x \in \mathbb{R}. \end{align*}\] en forme de cloche, est symmétrique autour de \(\mu\), qui est aussi le mode de la distribution.
The distribution function of the normal distribution is not available in closed-form. La loi normale est une famille de localisation échelle: si \(Y \sim \mathsf{normale}(\mu, \sigma^2)\), alors \(Z = (Y-\mu)/\sigma \sim \mathsf{normale}(0,1)\). Inversement, si \(Z \sim \mathsf{normale}(0,1)\), alors \(Y = \mu + \sigma Z \sim \mathsf{normale}(\mu, \sigma^2)\).
Nous verrons aussi l’extension multidimensionnelle de la loi normale: un \(d\) vecteur \(\boldsymbol{Y} \sim \mathsf{normal}_d(\boldsymbol{\mu}, \boldsymbol{\Sigma})\) admet une fonction de densité égale à \[\begin{align*} f(\boldsymbol{x}) = (2\pi)^{-d/2} |\boldsymbol{\Sigma}|^{-1/2} \exp \left\{ - \frac{1}{2} (\boldsymbol{x}-\boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right\} \end{align*}\]
Le vecteur de moyenne \(\boldsymbol{\mu}\) contient l’espérance de chaque composante, tandis que \(\boldsymbol{\Sigma}\) est la matrice de covariance de \(\boldsymbol{Y}\). Une propriété unique à la loi normale (muldimensionnelle) est le lien entre indépendance et matrice de covariance: si \(Y_i\) et \(Y_j\) sont indépendants, alors l’entrée \((i,j)\) hors diagonale de \(\boldsymbol{\Sigma}\) est nulle.
Les trois lois suivantes ne sont pas couvertes dans les cours d’introduction, mais elles interviennent régulièrement dans les cours de mathématique statistique et serviront d’étalon de mesure pour déterminer si les statistiques de test sont extrêmes sous l’hypothèse nulle.
Définition 1.10 (Loi khi-deux) La loi de khi-deux avec \(\nu>0\) degrés de liberté, dénotée \(\chi^2_{\nu}\) ou \(\mathsf{khi-deux}(\nu)\) joue un rôle important en statistique. Sa densité est \[\begin{align*} f(x; \nu) = \frac{1}{2^{\nu/2}\Gamma(\nu/2)}x^{\nu/2-1}\exp(-x/2),\qquad x >0. \end{align*}\] Elle est obtenue pour \(\nu\) entier en prenant la somme de variables normales centrées et réduites au carré: si \(Y_i \stackrel{\mathrm{iid}}{\sim}\mathsf{normale}(0,1)\) pour \(i=1, \ldots, k\), alors \(\sum_{i=1}^k Y_i^2 \sim \chi^2_k\). L’espérance de la loi \(\chi^2_k\) est \(k\).
Si on considère un échantillon aléatoire et identiquement distribution de \(n\) observations de lois normales, alors la variance empirique repondérée satisfait \((n-1)S^2/\sigma^2 \sim \chi^2_{n-1}\).
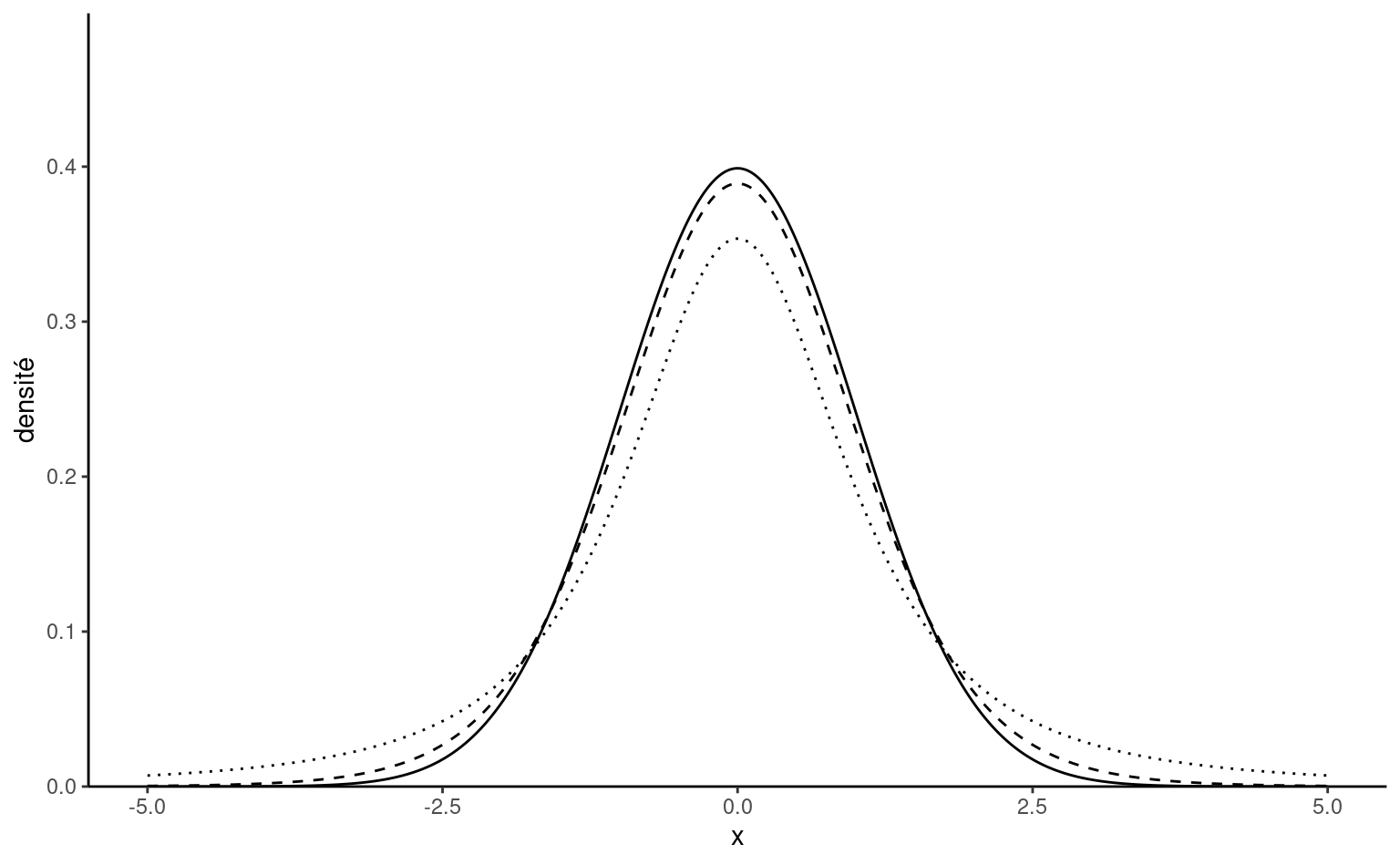
Définition 1.11 (Loi Student-\(t\)) La loi Student-\(t\) avec \(\nu>0\) degrés de liberté est une famille de localisation et d’échelle de densité symmétrique. On la dénote \(\mathsf{Student}(\nu)\) dans le cas centré réduit.
Son nom provient d’un article de William Gosset sous le pseudonyme Student (Gosset 1908), qui a introduit la loi comme approximation au comportement de la statistique \(t\). La densité d’une loi Student standard avec \(\nu\) degrés de liberté est \[\begin{align*} f(y; \nu) = \frac{\Gamma \left( \frac{\nu+1}{2}\right)}{\Gamma\left(\frac{\nu}{2}\right) \sqrt{\nu\pi}}\left(1+\frac{y^{2}}{\nu}\right)^{-\frac{\nu+1}{2}}. \end{align*}\] La loi a des ailes à décroissance polynomiale, est symmétrique autour de zéro et unimodale. Quand \(\nu \to \infty\), on recouvre une loi normale, mais les ailes sont plus lourdes que la loi normale. Effectivement, seuls les \(\nu-1\) premiers moments de la distribution existent: la loi \(\mathsf{Student}(2)\) n’a pas de variance.
Si les \(n\) observations indépendantes et identiquement distribuées \(Y_i \sim \mathsf{normale}(\mu, \sigma^2)\), alors la moyenne empirique centrée, divisée par la variance empirique, \((\overline{Y}-\mu)/S^2\), suit une loi Student-\(t\) avec \(n-1\) degrés de liberté.
Définition 1.12 (Loi de Fisher) La loi de Fisher, ou loi \(F\), sert à déterminer le comportement en grand échantillon de statistiques de test pour la comparaison de plusieurs moyennes (analyse de variance) sous un postulat de normalité des observations.
La loi \(F\), dite de Fisher et dénotée \(\mathsf{Fisher}(\nu_1, \nu_2)\), est obtenue en divisant deux variables khi-deux indépendantes de degrés de liberté \(\nu_1\) et \(\nu_2\). Spécifiquement, si \(Y_1 \sim \chi^2_{\nu_1}\) et \(Y_2 \sim \chi^2_{\nu_2}\), alors \[\begin{align*} F = \frac{Y_1/\nu_1}{Y_2/\nu_2} \sim \mathsf{Fisher}(\nu_1, \nu_2) \end{align*}\]
La loi de Fisher tend vers une loi \(\chi^2_{\nu_1}\) quand \(\nu_2 \to \infty\).
Cette section sert à réviser les principales représentations graphiques de jeux de données selon la catégorie des variables.
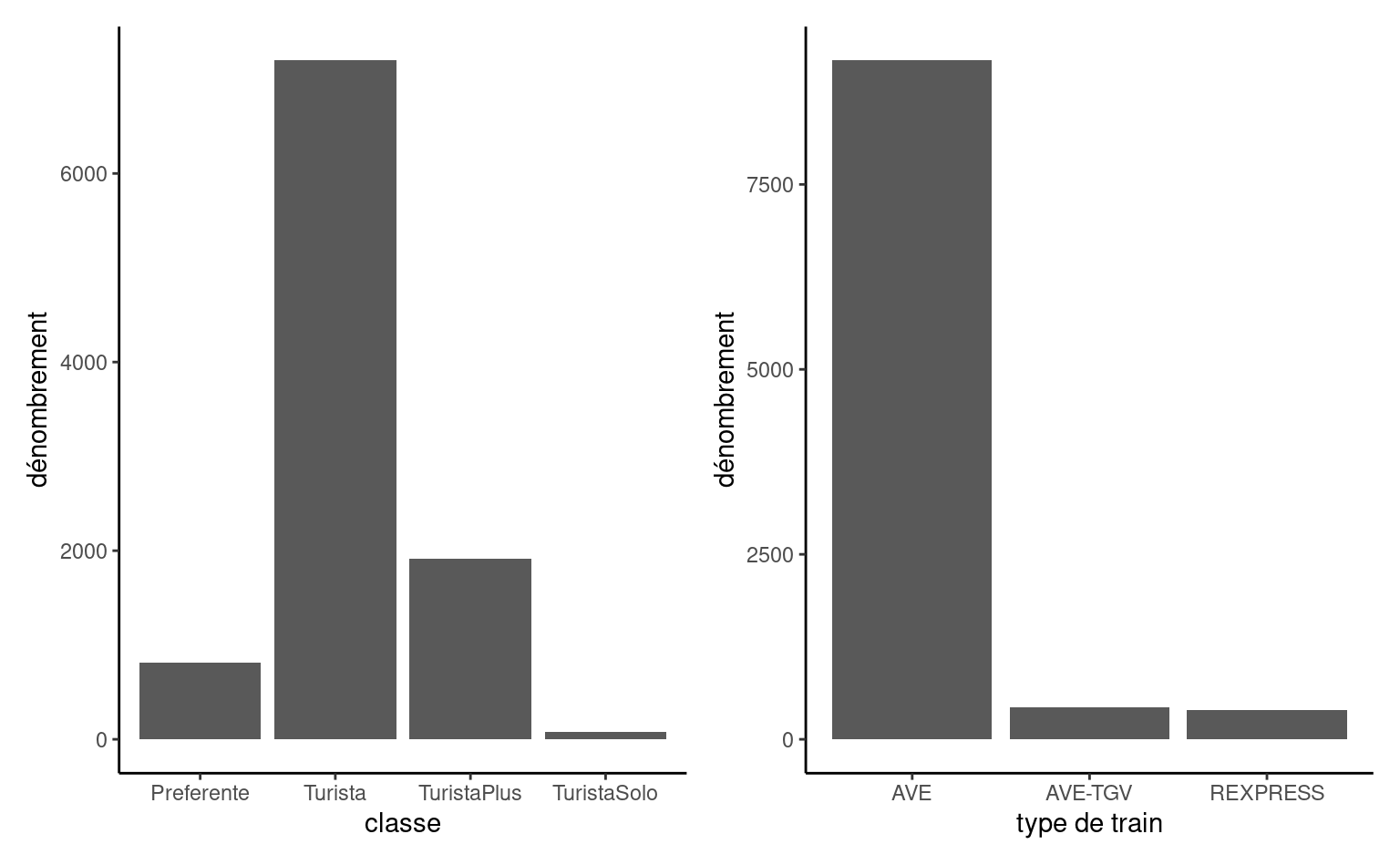
Le principal type de graphique pour représenter la distribution d’une variable catégorielle est le diagramme en bâtons, dans lequel la fréquence de chaque catégorie est présentée sur l’axe des ordonnées (\(y\)) en fonction de la modalité, sur l’axe des abscisses (\(x\)), et ordonnées pour des variables ordinales. Cette représentation est en tout point supérieur au diagramme en camembert, une engeance répandu qui devrait être honnie (notamment parce que l’humain juge mal les différences d’aires, qu’une simple rotation change la perception du graphique et qu’il est difficile de mesurer les proportions) — ce n’est pas de la tarte!
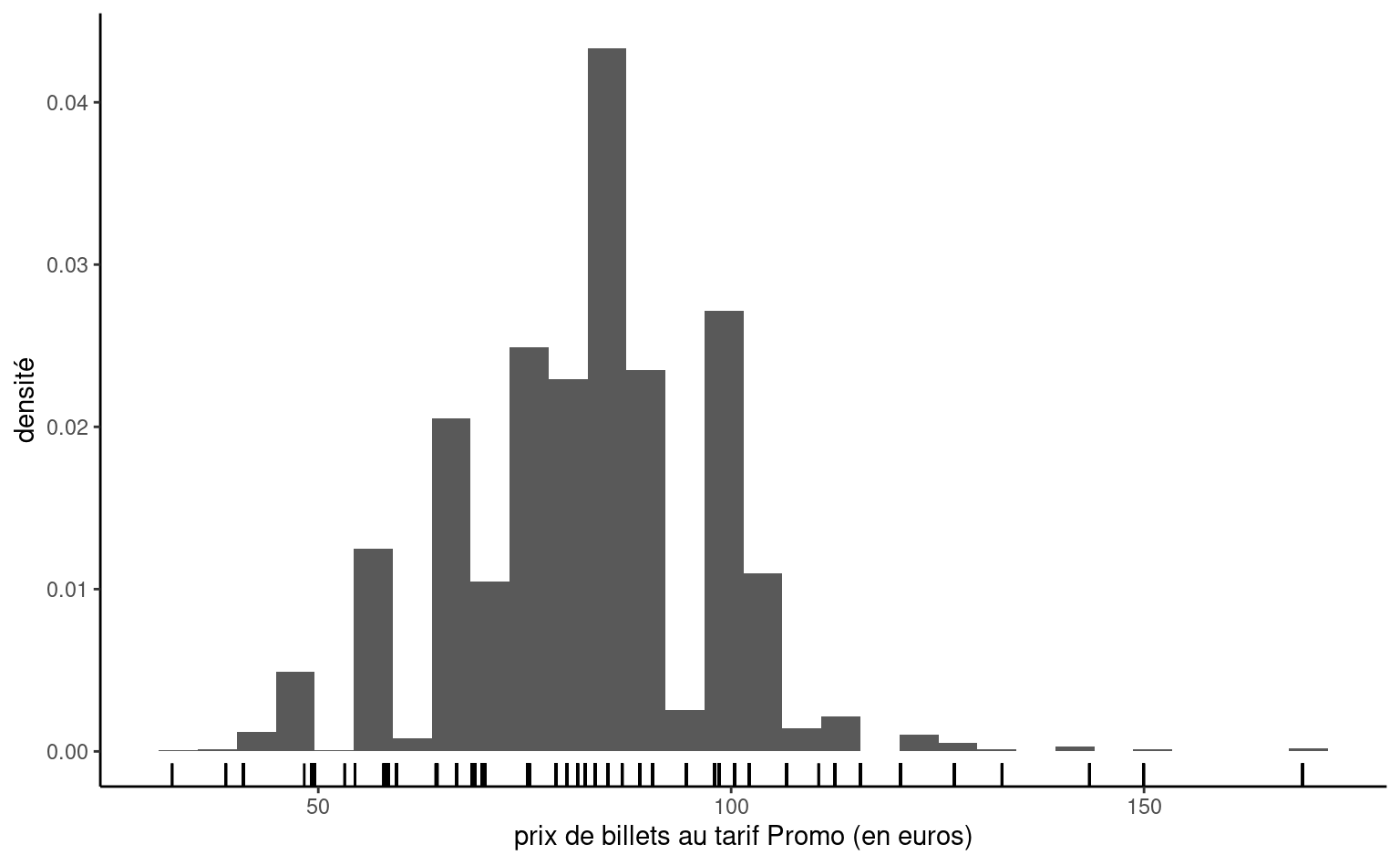
Puisque les variables continues peuvent prendre autant de valeurs distinctes qu’il y a d’observations, on ne peut simplement compter le nombre d’occurrence par valeur unique. On regroupera plutôt dans un certain nombre d’intervalle, en discrétisant l’ensemble des valeurs en classes pour obtenir un histogramme. Le nombre de classes dépendra du nombre d’observations si on veut que l’estimation ne soit pas impactée par le faible nombre d’observations par classe: règle générale, le nombre de classes ne devrait pas dépasser \(\sqrt{n}\), où \(n\) est le nombre d’observations de l’échantillon. On obtiendra la fréquence de chaque classe, mais si on normalise l’histogramme (de façon à ce que l’aire sous les bandes verticales égale un), on obtient une approximation discrète de la fonction de densité. Faire varier le nombre de classes permet parfois de faire apparaître des caractéristiques de la variable (notamment la multimodalité, l’asymmétrie et les arrondis).
Puisque qu’on groupe les observations en classe pour tracer l’histogramme, il est difficile de voir l’étendue des valeurs que prenne la variable: on peut rajouter des traits sous l’histogramme pour représenter les valeurs uniques prises par la variable, tandis que la hauteur de l’histogramme nous renseigne sur leur fréquence relative.
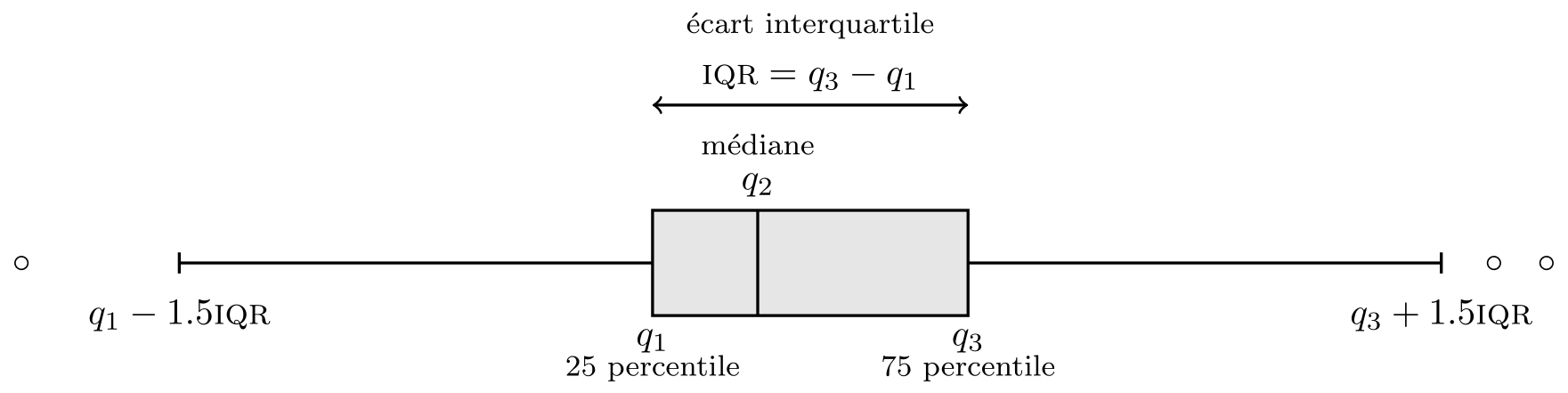
Définition 1.13 (Boîte à moustaches) Elle représente graphiquement cinq statistiques descriptives.
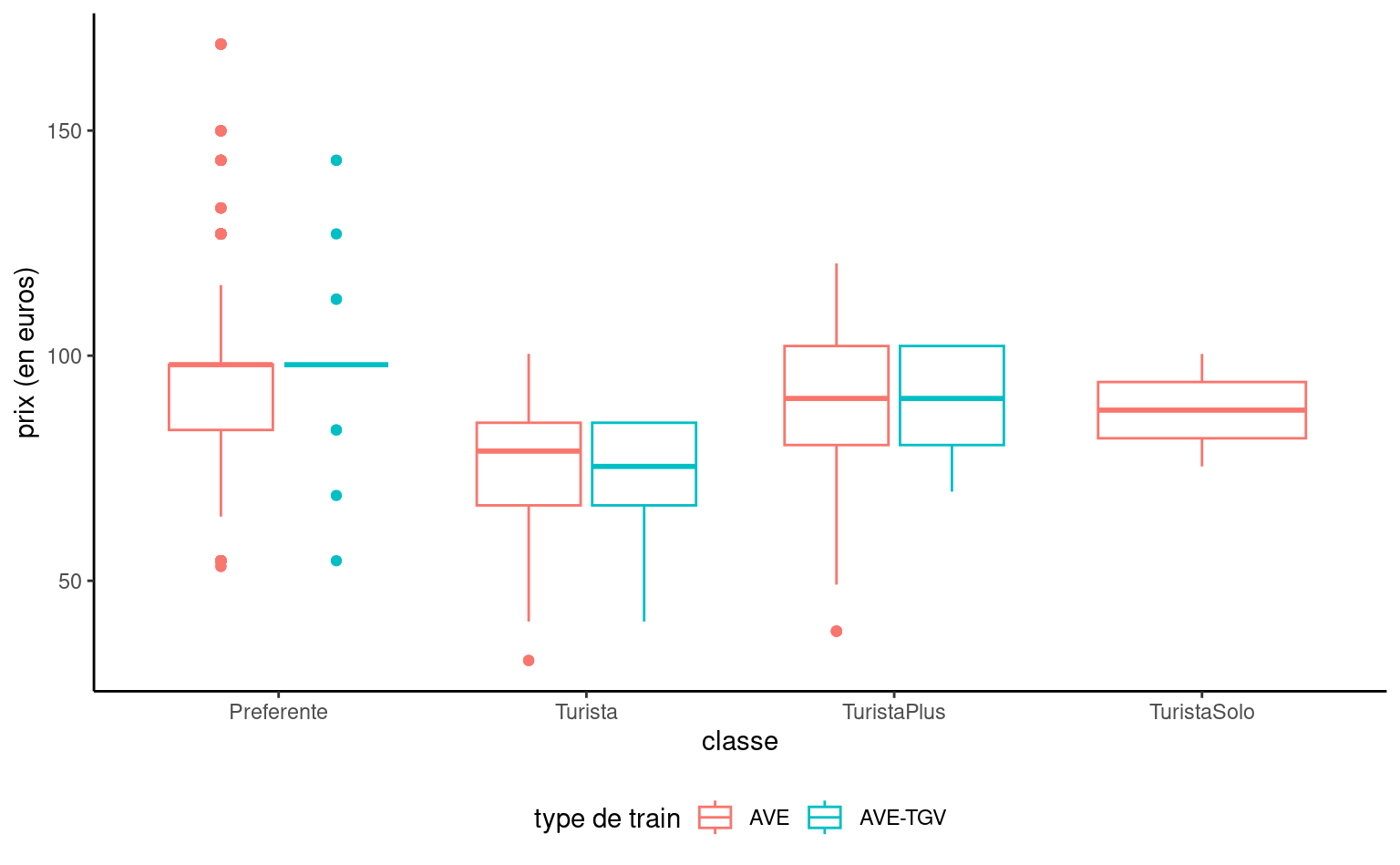
On peut représenter la distribution d’une variable réponse continue en fonction d’une variable catégorielle en traçant une boîte à moustaches pour chaque catégorie et en les disposant côte-à-côte. Une troisième variable catégorielle peut être ajoutée par le biais de couleurs, comme dans la Figure 1.8.
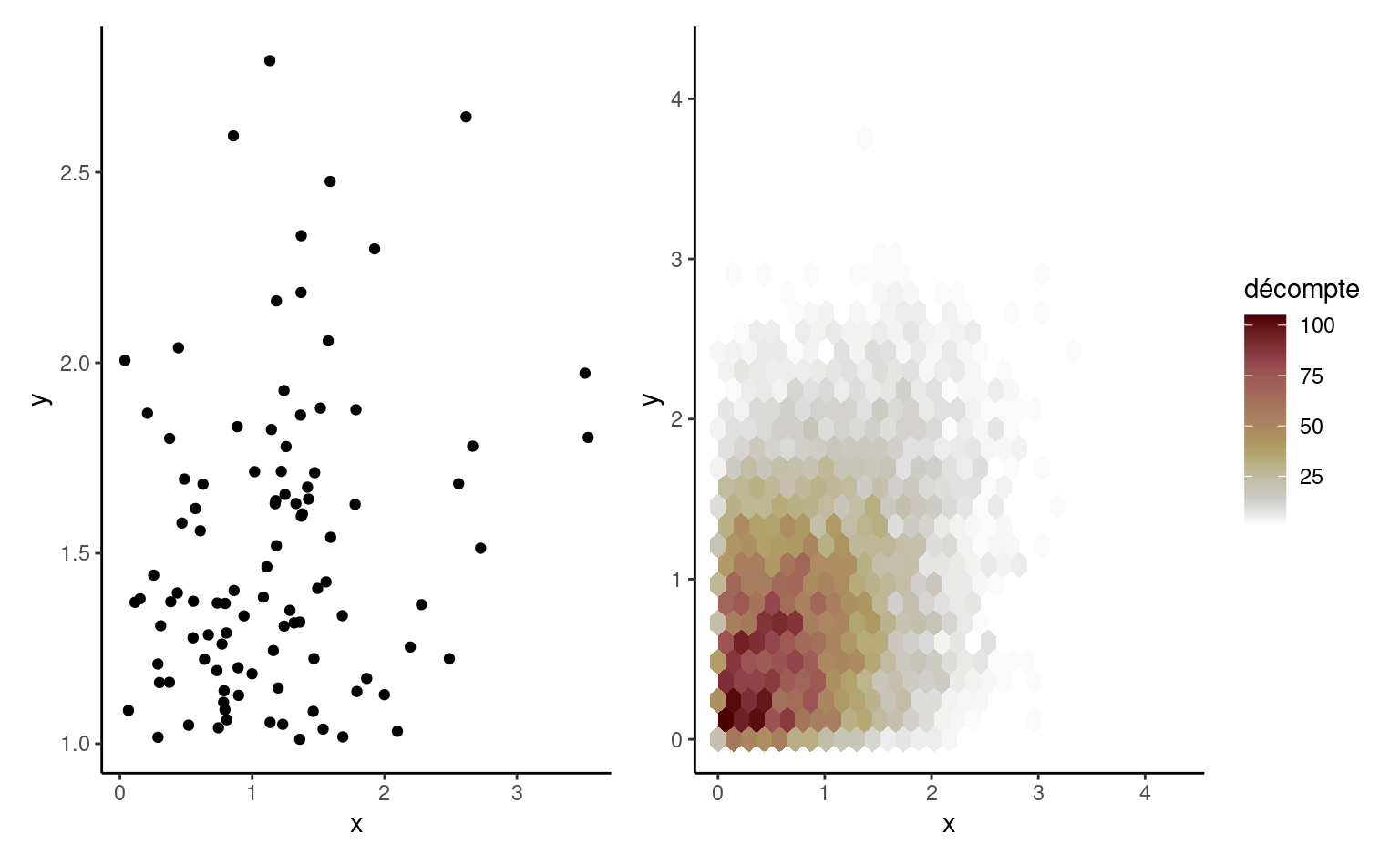
Si on veut représenter la covariabilité de deux variables continues, on utilise un nuage de points où chaque variable est représentée sur un axe et chaque observation donne la coordonnée des points. Si la représentation graphique est dominée par quelques valeurs très grandes, une transformation des données peut être utile: vous verrez souvent des données positives à l’échelle logarithmique. Si le nombre d’observations est très grand, il devient difficile de distinguer quoi que ce soit. On peut alors ajouter de la transparence ou regrouper des données en compartiments bidimensionnels (un histogramme bidimensionnel), dont la couleur représente la fréquence de chaque compartiment. Le paneau gauche de Figure 1.9 montre un nuage de points de 100 observations simulées, tandis que celui de droite représente des compartiments hexagonaux contenant 10 000 points.
Si on ajuste un modèle à des données, il convient de vérifier la qualité de l’ajustement et l’adéquation du modèle, par exemple graphiquement.
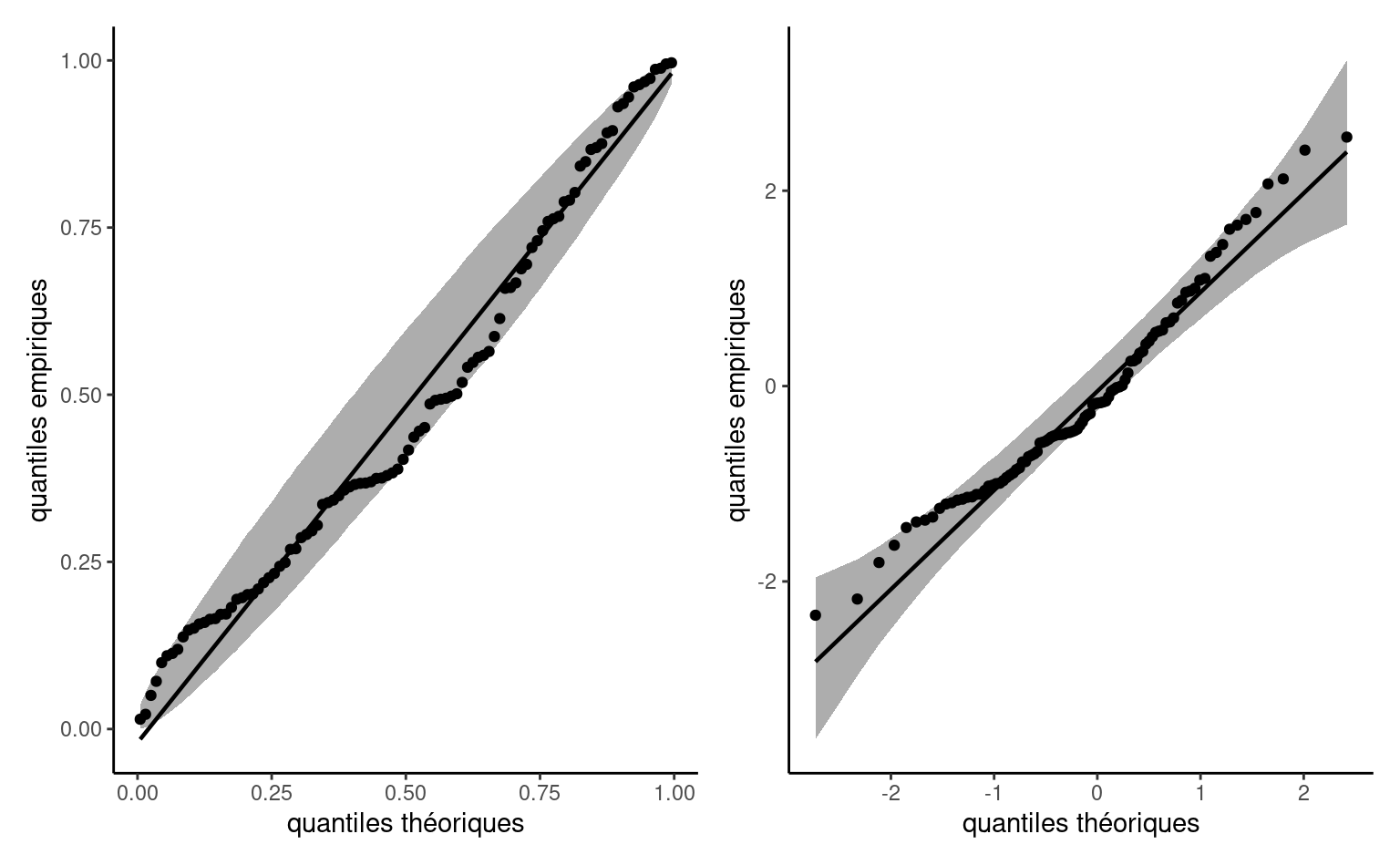
Définition 1.14 (Diagrammes quantiles-quantiles) Le diagramme quantile-quantile sert à vérifier l’adéquation du modèle et découle du constat suivant: si \(Y\) est une variable aléatoire continue et \(F\) sa fonction de répartition, alors l’application \(F(Y) \sim \mathsf{unif}(0,1)\), une loi uniforme standard. De la même façon, appliquer la fonction quantile à une variable uniforme permet de simuler de la loi \(F\), et donc \(F^{-1}(U)\). Supposons un échantillon uniforme de taille \(n\). On peut démontrer que, pour des variables continues, les statistiques d’ordre \(U_{(1)} \leq \cdots \leq U_{(n)}\) ont une loi marginale beta, avec \(U_{(k)} \sim \mathsf{Beta}(k, n+1-k)\) d’espérance \(k/(n+1)\).
Les paramètres de la loi \(F\) sont inconnus, mais on peut obtenir un estimateur \(\widehat{F}\) et appliquer la transformation inverse pour obtenir une variable approximativement uniforme. Un diagramme quantile-quantile représente les données en fonction des moments des statistiques d’ordre transformées
Si le modèle est adéquat, les valeurs ordonnées devraient suivre une droite de pente unitaire qui passe par l’origine. Le diagramme probabilité-probabilité représente plutôt les données à l’échelle uniforme \(\{\mathrm{rang}(Y_i)/(n+1), \widehat{F}(Y_i)\}\).
Même si on connaissait exactement la loi aléatoire des données, la variabilité intrinsèque à l’échantillon fait en sorte que des déviations qui semblent significatives et anormales à l’oeil de l’analyste sont en fait compatibles avec le modèle: un simple estimé ponctuel sans mesure d’incertitude ne permet donc pas facilement de voir ce qui est plausible ou pas. On va donc idéalement ajouter un intervalle de confiance (approximatif) ponctuel ou conjoint au diagramme.
Pour obtenir l’intervalle de confiance approximatif, la méthode la plus simple est par simulation, en répétant \(B\) fois les étapes suivantes
Le résultat de cette opération sera une matrice \(n \times B\) de données simulées; on obtient un intervalle de confiance symmétrique en conservant le quantile \(\alpha/2\) et \(1-\alpha/2\) de chaque ligne. Le nombre de simulation \(B\) devrait être large (typiquement 999 ou davantage) et être choisi de manière à ce que \(B/\alpha\) soit un entier.
Pour l’intervalle de confiance ponctuel, chaque valeur représente une statistique et donc individuellement, la probabilité qu’une statistique d’ordre sorte de l’intervalle de confiance est \(\alpha\). En revanche, les statistiques d’ordres ne sont pas indépendantes et sont qui est plus ordonnées, ce qui fait qu’un point hors de l’intervalle risque de n’être pas isolé. Les intervalles présentés dans la Figure 1.10 sont donc ponctuels. La variabilité des statistiques d’ordre uniformes est plus grande autour de 1/2, mais celles des variables transformées dépend de \(F\).
L’interprétation d’un diagramme quantile-quantile nécessite une bonne dose de pratique et de l’expérience: cette publication par Glen_b sur StackOverflow résume bien ce qu’on peut détecter ou pas en lisant le diagramme.
Un estimateur est dit convergent si la valeur obtenue à mesure que la taille de l’échantillon augmente s’approche de la vraie valeur que l’on cherche à estimer. Mathématiquement parlant, un estimateur est dit convergent s’il converge en probabilité, ou \(\hat{\theta} \stackrel{\mathsf{Pr}}{\to} \theta\): en langage commun, la probabilité que la différence entre \(\hat{\theta}\) et \(\theta\) diffèrent est négligeable quand \(n\) est grand.
La condition a minima pour le choix d’un estimateur est donc la convergence: plus on récolte d’information, plus notre estimateur devrait s’approcher de la valeur qu’on tente d’estimer.
La loi des grands nombres établit que la moyenne empirique de \(n\) observations indépendantes de même espérance, \(\overline{Y}_n\), tend vers l’espérance commune des variables \(\mu\), où \(\overline{Y}_n \rightarrow \mu\). En gros, ce résultat nous dit que l’on réussit à approximer de mieux en mieux la quantité d’intérêt quand la taille de l’échantillon (et donc la quantité d’information disponible sur le paramètre) augmente. La loi des grands nombres est très utile dans les expériences Monte Carlo: on peut ainsi approximer par simulation la moyenne d’une fonction \(g(x)\) de variables aléatoires en simulant de façon répétée des variables \(Y\) indépendantes et identiquement distribuées et en prenant la moyenne empirique \(n^{-1} \sum_{i=1}^n g(Y_i)\).
Si la loi des grands nombres nous renseigne sur le comportement limite ponctuel, il ne nous donne aucune information sur la variabilité de notre estimé de la moyenne et la vitesse à laquelle on s’approche de la vraie valeur du paramètre.
Le théorème central limite dit que, pour un échantillon aléatoire de taille \(n\) dont les observations sont indépendantes et tirées d’une loi quelconque d’espérance \(\mu\) et de variance finie \(\sigma^2\), alors la moyenne empirique tend non seulement vers \(\mu\), mais à une vitesse précise:
Mathématiquement, le théorème central limite dicte que \(\sqrt{n}(\overline{Y}-\mu) \stackrel{\mathrm{d}}{\rightarrow} \mathsf{normale}(0, \sigma^2)\). Si \(n\) est grand (typiquement supérieur à \(30\), mais cette règle dépend de la loi sous-jacente de \(Y\)), alors \(\overline{Y} \stackrel{\cdot}{\sim} \mathsf{normale}(\mu, \sigma^2/n)\).
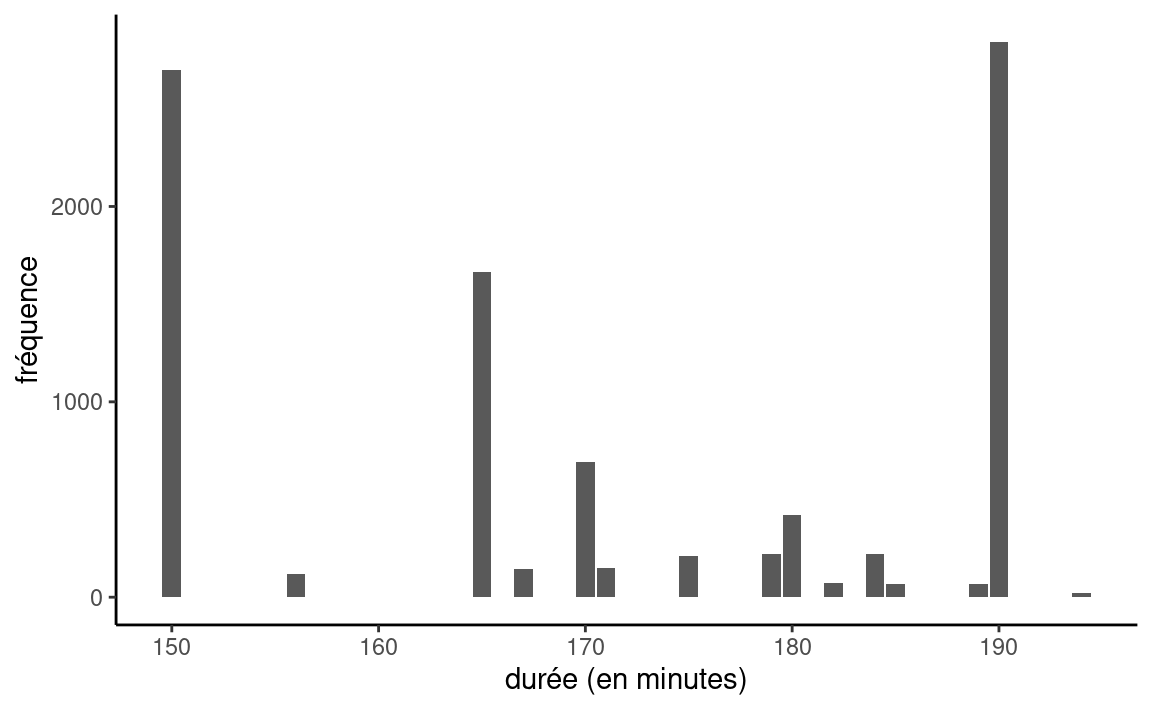
Comment interpréter ce résultat? On considère comme exemple le temps de trajet moyen de trains à haute vitesse AVE entre Madrid et Barcelone opérés par la Renfe.
Une analyse exploratoire indique que la durée du trajet de la base de données est celle affichée sur le billet (et non le temps réel du parcours). Ainsi, il n’y a ainsi que 15 valeurs possibles. Le temps affiché moyen pour le parcours, estimé sur la base de 9603 observations, est de 170 minutes et 41 secondes. La Figure 1.11 montre la distribution empirique des données.
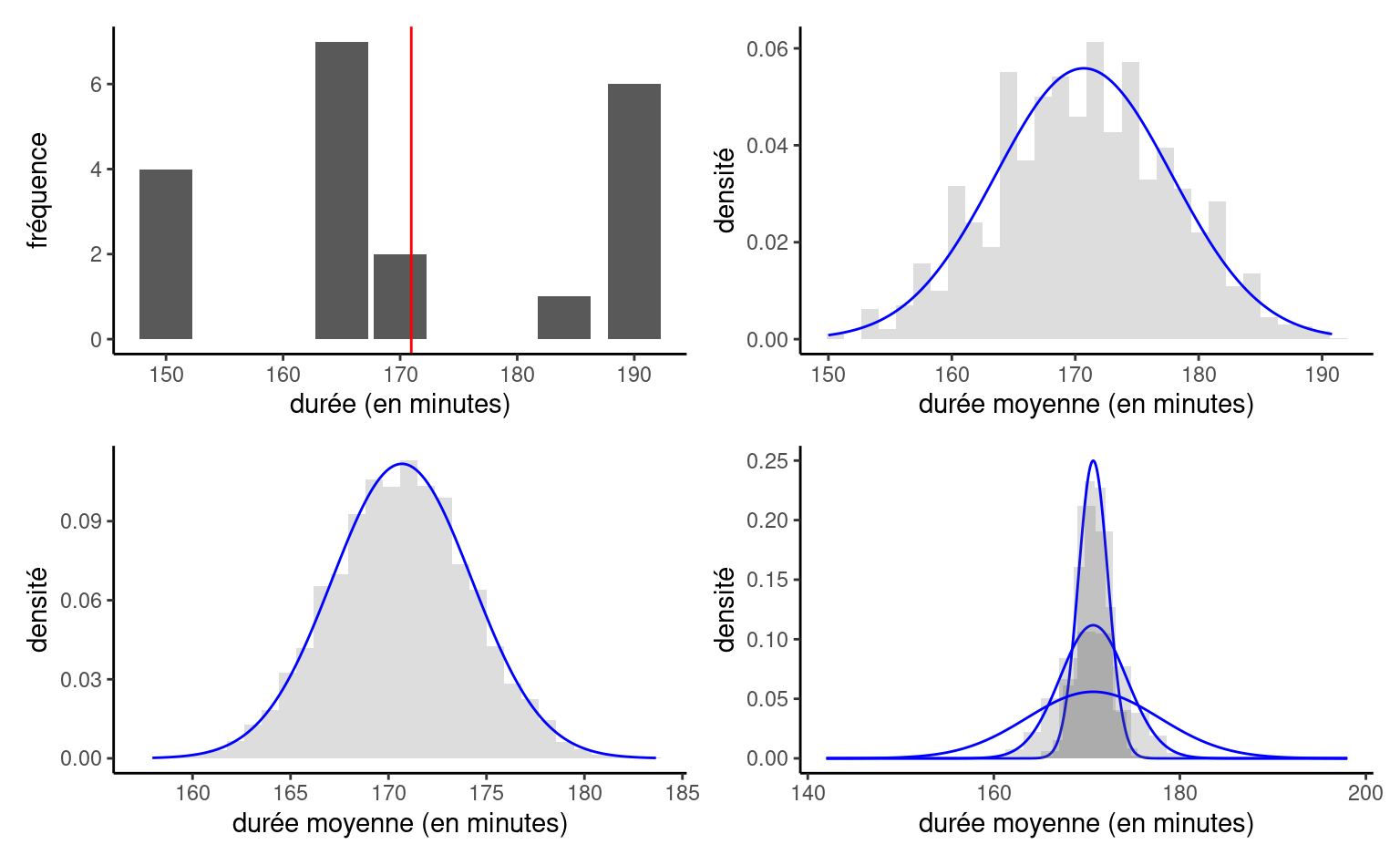
Considérons maintenant des échantillons de taille \(n=10\). Dans notre premier échantillon aléatoire, la durée moyenne affichée est 169.3 minutes, elle est de 167 minutes dans le deuxième, de 157.9 dans le troisième, et ainsi de suite.
Supposons qu’on tire \(B=1000\) échantillons différents, chacun de taille \(n=5\), de notre ensemble, et qu’on calcule la moyenne de chacun d’entre eux. Le graphique supérieur droit de la Figure 1.12 montre un de ces 1000 échantillons aléatoire de taille \(n=20\) tiré de notre base de données. Les autres graphiques de la Figure 1.12 illustrent l’effet de l’augmentation de la taille de l’échantillon: si l’approximation normale est approximative avec \(n=5\), la distribution des moyennes est virtuellement identique à partir de \(n=20\). Plus la moyenne est calculée à partir d’un grand échantillon (c’est-à-dire, plus \(n\) augmente), plus la qualité de l’approximation normale est meilleure et plus la courbe se concentre autour de la vraie moyenne; malgré le fait que nos données sont discrètes, la distribution des moyennes est approximativement normale.
On a considéré une seule loi aléatoire inspirée de l’exemple, mais vous pouvez vous amuser à regarder l’effet de la distribution sous-jacent et de la taille de l’échantillon nécessaire pour que l’effet du théorème central limite prenne effet: il suffit pour cela de simulant des observations d’une loi quelconque de variance finie, en utilisant par exemple cette applette.
Les statistiques de test qui découlent d’une moyenne centrée-réduite (ou d’une quantité équivalente pour laquelle un théorème central limite s’applique) ont souvent une loi nulle standard normale, du moins asymptotiquement (quand \(n\) est grand, typiquement \(n>30\) est suffisant). C’est ce qui garantie la validité de notre inférence!