Tests d’hypothèse

Exercice 1.1

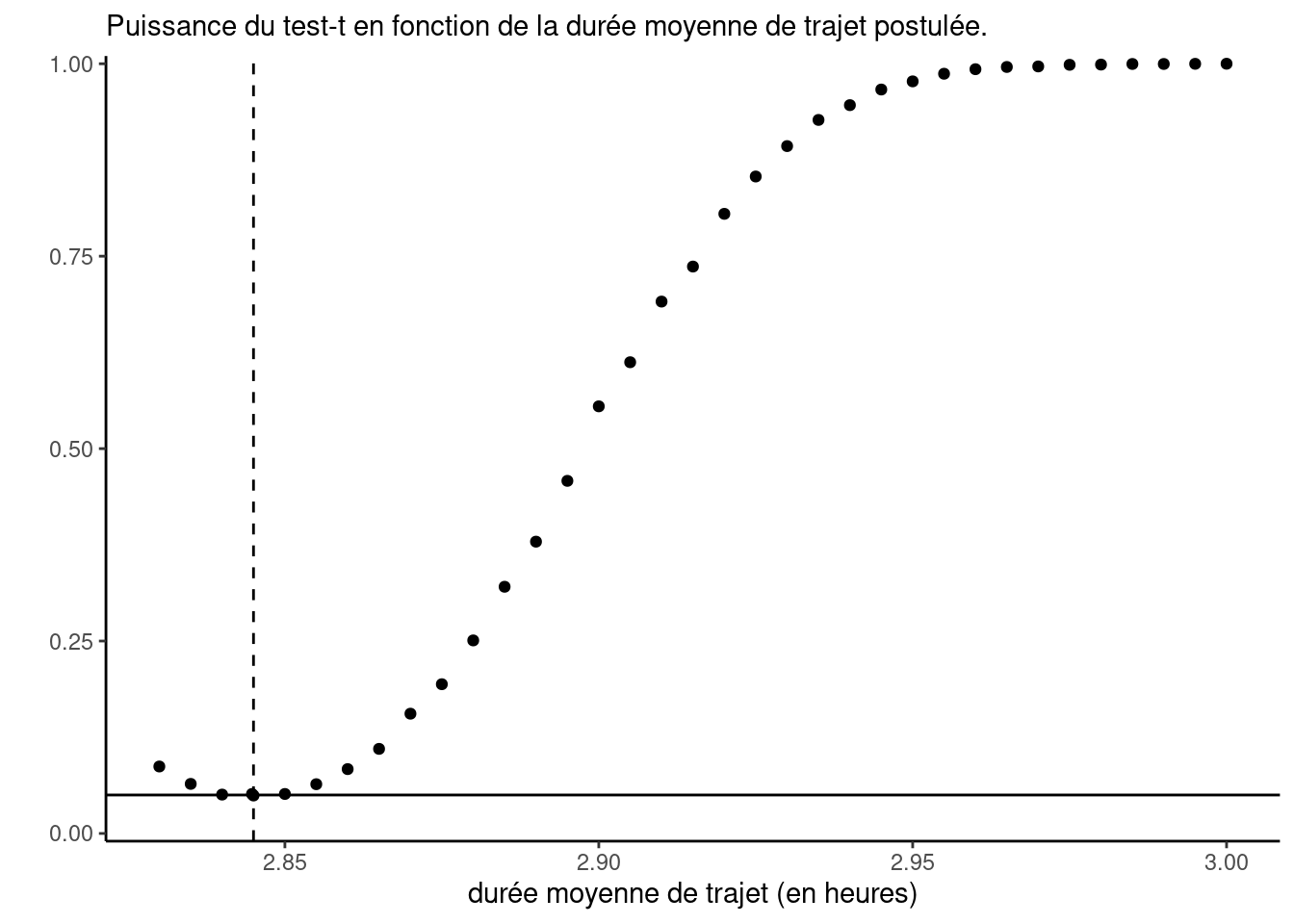
  1. Expliquez pourquoi la proportion de rejet de chaque test augmente quand on se déplace vers la droite sur le graphique.
  2. Supposez que l’on répète l’expérience de simulation, mais cette fois avec des sous-échantillons aléatoires de taille \(n=1000\). Comment est-ce que les points pour le test-\(t\) pour un échantillon se compareraient à ceux tracés sur le graphique? Seraient-ils en dessous, à la même hauteur ou au dessus?
  3. Expliquez pourquoi la valeur sur le graphique ppour un échantillon devrait être approximativement 0.05 dans un voisinage de \(\mu=2,845\).
  4. Produisez un diagramme quantile-quantile normal et commentez sur la robustesse du test-\(t\) à des déviations de l’hypothèse de normalité.

Solution 1.

  1. La courbe donne le pourcentage de rejet de l’hypothèse nulle pour le test-\(t\) pour un échantillon. Le plus on s’éloigne de la vraie valeur \(\mu\), le plus de preuves on accumule pour détecter un départ de l’hypothèse nulle \(\mathscr{H}_0\). Elle tend vers 0.05 près de \(\mu\) et augmente vers un des deux côtés à mesure que l’on s’éloigne de la vraie moyenne.
  2. La puissance augmente si \(n\) croît, donc on s’attend que la courbe soit au dessus partout, sauf dans un voisinage de \(\mu\) où elle devrait demeurer approximativement 0.05 si les hypothèses du test sont respectées.
  3. Puisque le test est fait à niveau \(\alpha=0.05\), on devrait recouvrer le niveau du test quand \(\mathscr{H}_0\) est vraie.
  4. Les données ne sont pas normalement distribuées et fortement discrétisées, mais la courbe de puissance du test-\(t\) pour un échantillon semble augmenter à mesure que l’on s’éloigne de \(\mu\) et le niveau nominal du test correspond au niveau empirique, ou erreur de type I. Cela illustre la robustesse du test au départ de la normalité et c’est une conséquence du théorème central limite.
Figure 1: Courbe de puissance pour le test-\(t\) pour un échantillon en fonction du temps de parcours (en heures). La ligne horizontale grise est située à 0.05, tandis que la ligne traitillée verticale marque la vraie moyenne \(\mu\).

Exercice 1.2

Supposez que l’on veut comparer le tarif moyen pour les trains à grande vitesse pour les deux destinations, soit de Madrid vers Barcelone et le trajet inverse de Barcelone à Madrid. Une étude de simulation a été réalisée dans laquelle le test de Welch pour deux échantillons a été calculé sur des sous-échantillons aléatoires de taille \(n=1000\). Les données renfe_simu contiennent les différences moyennes (difmoy), les statistiques de test (Wstat), les valeurs-\(p\) (valp) et les intervalles de confiance à 95% (icbi et icbs) pour 1000 répétitions. Supposez que l’on sait que la vraie différence moyenne dans la population est de \(-0,28\)€. Utilisez les données simulées pour répondre aux questions suivantes et commentez brièvement sur chaque sous-question.

  1. Quel est le taux de couverture empirique des intervalles de confiance à 95% (c’est-à-dire le pourcentage des intervalles couvrant la valeur de la « vraie » différence moyenne)?
  2. Tracez un histogramme des différences moyennes et superposez la vraie différence moyenne à l’aide d’un trait vertical.
  3. Calculez la puissance du test (pourcentage de rejet de l’hypothèse nulle sous l’hypothèse alternative).

Solution 2.

  1. Le taux de couverture empirique est 0.947; cette valeur est près du taux de couverture théorique nominal, ce qui indique que le test est bien calibré.
Code 
data(renfe_simu, package = "hecmodstat")
vraie_diff <- -0.28
couverture <- mean(with(renfe_simu, icbi < vraie_diff & icbs > vraie_diff))
couverture
[1] 0.947
  1. Figure 2 contient deux histogrammes: la différence moyenne semble approximativement normale et centrée en \(0.28\), tandis que les valeurs-\(p\) sont réparties dans l’intervalle \([0,1]\) avec plus de valeurs près de zéro.
Code 
library(ggplot2)
library(patchwork) 
theme_set(theme_classic())
g1 <- ggplot(data = renfe_simu, 
             mapping = aes(x = difmoy)) +
  geom_density() +
  geom_vline(xintercept = vraie_diff, 
             color = "gray",
             linetype = "dashed") +
  scale_y_continuous(limits = c(0,NA), expand = expansion()) + 
  labs(x = "moyenne des différences")
g2 <- ggplot(data = renfe_simu,
             mapping = aes(x = valp)) +
  geom_histogram(bins = 11) +
  scale_y_continuous(limits = c(0,NA), expand = expansion())
g1 + g2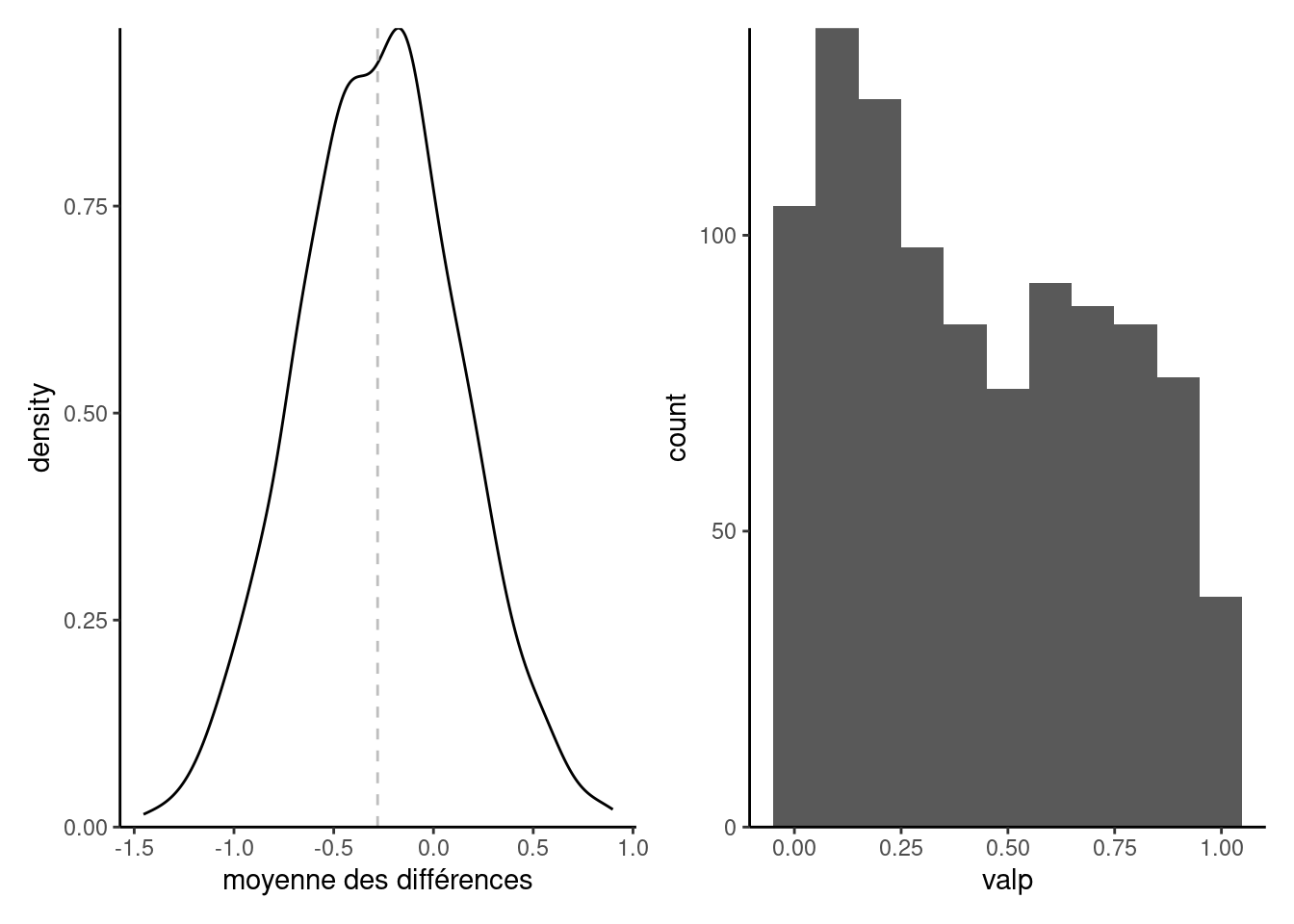
Figure 2: Gauche: densité de la différence moyenne de prix pour les trains à grande vitesse entre Madrid et Barcelone, versus Barcelone et Madrid. La vraie différence de moyenne est montrée par une ligne verticale. Droite: histogramme des valeurs-p.
  1. La puissance est \(0.105\). Sous le régime alternatif (puisque \(\Delta=0.28\)€), on rejette 10.5% du temps l’hypothèse nulle. Ce pourcentage est faible parce que la différence est petite et donc difficile de distinguer cette différence de la variabilité intrinsèque de la statistique à moins d’avoir une grande taille d’échantillon. La différence moyenne estimée avec l’échantillon est de \(0.274\).
Code 
mean(renfe_simu$valp < 0.05)
[1] 0.105

Exercice 1.3

À l’aide des données renfe, testez si le prix moyen du billet pour un train de classe AVE-TGV est le même que celui d’un train régio-express (REXPRESS). Veillez à

  • énoncer l’hypothèse nulle et l’hypothèse alternative,
  • justifier avec soin le choix de votre statistique de test,
  • rapporter la différence moyenne estimée et un intervalle à 90% pour cette différence,
  • conclure dans le cadre de la mise en situation.

Solution 3. Le prix des billets REXPRESS est fixe et vaut 43.25€, on a donc un échantillon aléatoire que pour l’autre classe de train!

  • Soit \(\mu_{\text{AVE-TGV}}\) le prix moyen de l’ensemble des billets de train haute vitesse AVE-TGV.
  • L’hypothèse nulle est \(\mathscr{H}_0: \mu_{\text{AVE-TGV}}=43.25\)€ contre l’alternative \(\mathscr{H}_a: \mu_{\text{AVE-TGV}}\neq 43.25\)€.
  • Puisqu’on veut comparer la moyenne et qu’un seul échantillon est aléatoire, on utilise un test-\(t\) pour un échantillon.
  • La différence moyenne estimée est \(45.63\)€\(= 88.88\)€\(-43.25\)€, avec un intervalle de confiance à 90% pour la différence moyenne de \([44.14, 47.12]\).
  • La statistique \(t\), qui vaut 50.519 ici, suit une loi Student-\(t\) avec 428 degrés de liberté; une approximation normale serait identique. La valeur-\(p\) associée est négligeable, on conclut que le prix des trains AVE-TGV et REXPRESS diffèrent.
Code 
data(renfe, package = "hecmodstat")
library(dplyr)
renfe |> 
  group_by(type) |> 
  summarize(moy = mean(prix), sd = sd(prix))
# A tibble: 3 × 3
  type       moy    sd
  <fct>    <dbl> <dbl>
1 AVE       87.8  20.3
2 AVE-TGV   88.9  18.7
3 REXPRESS  43.2   0
Code 
testt <- with(renfe |> dplyr::filter(type == "AVE-TGV"),
     t.test(prix, mu = 43.25))
# Intervalle de confiance pour la différence
testt$conf.int - 43.25
[1] 43.85496 47.40560
attr(,"conf.level")
[1] 0.95