Statistical inference

The renfe data contains information about 10 000 train ticket sales from Renfe, the Spanish national train company. The data include:

Exercise 1.1

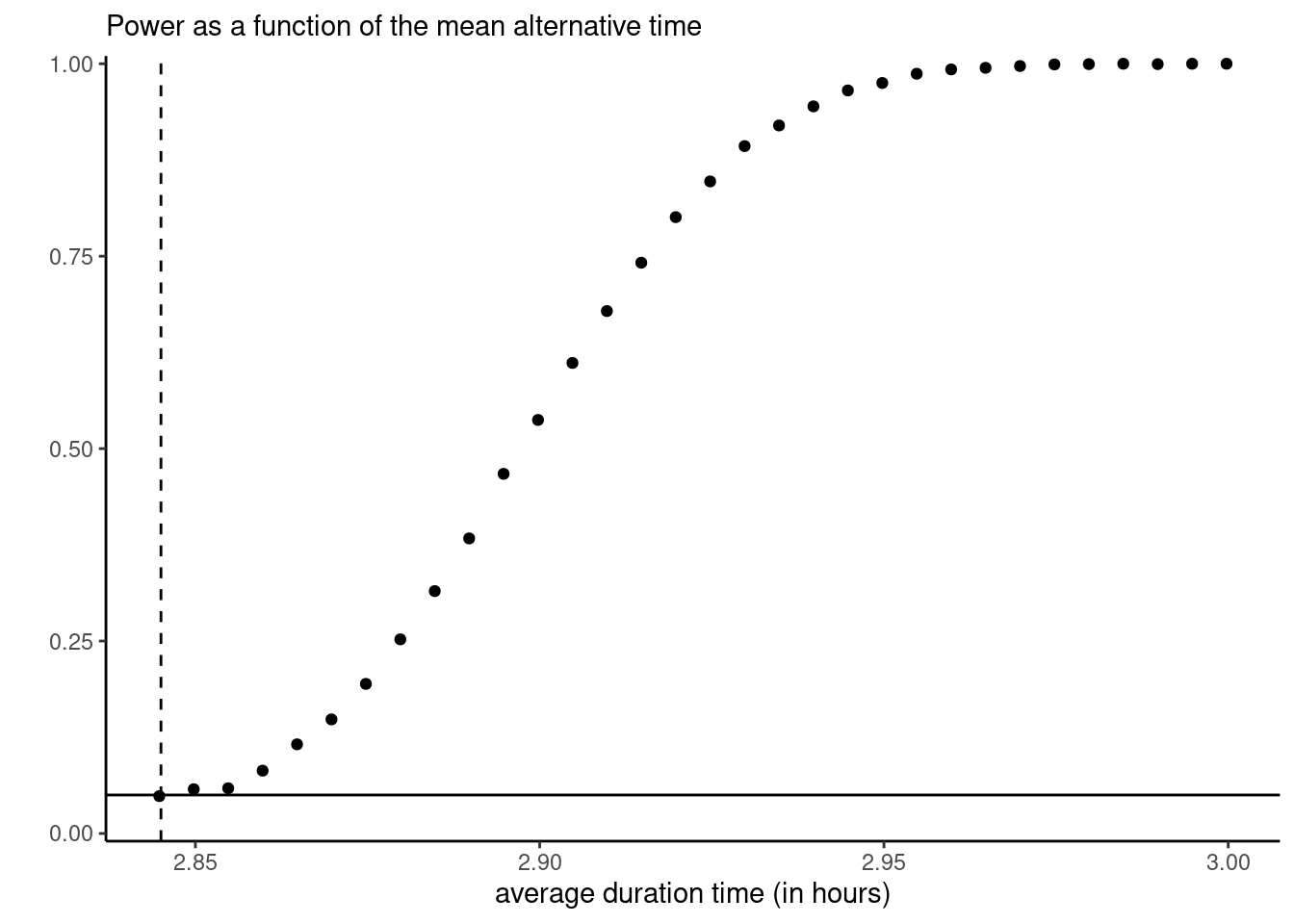
We consider travel time for high-speed (AVE and AVE-TGV) trains. The true “population” mean travel time between cities is known to be \(\mu=2.845\) hours (the instructor has access to the full dataset of more than 2.3 millions records, so these are known quantities, unlike in most practical settings).

A simulation study is performed to assess the behaviour of univariate tests under repeated sampling. The following algorithm was repeated 10K times for different values of \(\mu_0\):

  1. Select a random subsample of size \(n=100\).
  2. Compute the one-sample \(t\)-test statistic for \(\mathscr{H}_0: \mu=\mu_0\) (versus \(\mathscr{H}_0: \mu \neq \mu_0\)) .
  3. Return the \(p\)-value

Figure 1 shows the percentage of the 10K \(p\)-values that are less than 0.05, i.e. the percentage of rejection (at the \(5\)% level) of \(\mathscr{H}_0:\mu=\mu_0\) against the two-sided alternative at \(\mu_0 \in \{2.83, \nu, 2.835, 2.84, \ldots, 2.995, 3\`\). Use the resulting curve to answer the following questions:

Figure 1: Power curve for the one-sample \(t\)-test based on subsamples of size \(n=100\), as a function of travel time. The grey horizontal line is at 0.05, the vertical dashed line indicates the population mean \(\mu\).
  1. Explain why the value for the one-sample \(t\)-test around \(\mu=2.845\) should be approximately 0.05.
  2. Explain why the values on the curve increase towards the right of the plot.
  3. Suppose we repeated the simulation study, but this time with subsamples of size \(n=1000\). How would the points compare for the one-sample \(t\)-test: should they be higher, equal, or lower than their current values?
  4. Is the assumption of the one-sample \(t\)-test valid in this example? Produce a quantile-quantile plot using the code below and hence comment on the robustness of the \(t\)-test to departures from the normality assumption.

Exercise 1.2

Suppose we now want to compare the mean fare for high-speed train tickets for the two destinations, i.e., Madrid to Barcelona versus Barcelona to Madrid. We run a simulation study where we perform a two-sided Welch test for this hypothesis repeatedly with random subsamples of size \(n=1000\). The data renfe_simu contains the mean difference (meandif), the test statistic (Wstat), the \(p\)-value (pval) and the confidence interval (cilb and ciub) for these 1000 repetitions. Based on the entire database, the true mean difference is known to be \(-0.28\)€. Use the simulated data to answer the following questions and briefly comment on each item

  1. What is the empirical coverage of the 95% confidence intervals (i.e., the percentage of intervals covering the true mean difference value)?
  2. Plot an histogram of the mean differences and superimpose the true mean difference in the population.
  3. Compute the power of the test (percentage of rejection of the null hypothesis).

Exercise 1.3

Using the renfe data, test whether the average ticket price of AVE-TGV trains is different from that of Regio Express trains (REXPRESS). Make sure to

  • State your null and alternative hypothesis.
  • Carefully justify your choice of test statistic.
  • Report the estimated mean difference and a 90% confidence interval for that difference.
  • Conclude within the setting of the problem.