3 Priors
The posterior distribution combines two ingredients: the likelihood and the prior. If the former is a standard ingredient of any likelihood-based inference, prior specification requires some care. The purpose of this chapter is to consider different standard way of constructing prior functions, and to specify the parameters of the latter: we term these hyperparameters.
The posterior is a compromise prior and likelihood: the more informative the prior, the more the posterior resembles it, but in large samples, the effect of the prior is often negligible if there is enough information in the likelihood about all parameters. We can assess the robustness of the prior specification through a sensitivity analysis by comparing the outcomes of the posterior for different priors or different values of the hyperparameters.
Oftentimes, we will specify independent priors in multiparameter models, but the posterior of these will not be independent.
We can use moment matching to get sensible values, or tune via trial-and-error using the prior predictive draws to assess the implausibility of the prior outcomes. One challenge is that even if we have some prior information (e.g., we can obtain sensible prior values for the mean, quantiles or variance of the parameter of interest), these summary statisticss will not typically be enough to fully characterize the prior: many different functions or distributions could encode the same information. This means that different analysts get different inferences. Generally, we will choose the prior for convenience. Priors are controversial because they could be tuned aposteriori to give any answer an analyst might want.
At the end of the chapter, students should be able to
- define and distinguish between improper, weak and informative priors.
- propose conjugate priors for exponential families.
- assess by using the prior predictive distribution the compatibility of the prior with the model.
- use moment matching to specify the parameters of a prior distribution.
- perform sensitivity analysis by running a model with different priors and assessing changes to the posterior distribution.
3.1 Prior simulation
Expert elicitation is difficult and it is hard to grasp what the impacts of the hyperparameters are. One way to see if the priors are reasonable is to sample values from them and generate new observations, resulting in prior predictive draws.
The prior predictive is \(\int_{\boldsymbol{\Theta}} f(y_{\text{new}}; \boldsymbol{\theta}) p(\boldsymbol{\theta}) \mathrm{d} \boldsymbol{\theta}\): we can simulate outcomes from it by first drawing parameter values \(\boldsymbol{\theta}_0\) from the prior, then sampling new observations from the distribution \(f(y_{\text{new}}; \boldsymbol{\theta}_0)\) with those parameters values and keeping only \(y_{\text{new}}.\) If there are sensible bounds for the range of the response, we could restrict the prior range and shape until values abide to these.
Working with standardized inputs \(x_i \mapsto (x_i - \overline{x})/\mathrm{sd}(\boldsymbol{x})\) is useful. For example, in a simple linear regression (with a sole numerical explanatory), the slope is the correlation between standardized explanatory \(\mathrm{X}\) and standardized response \(Y\) and the intercept should be mean zero.
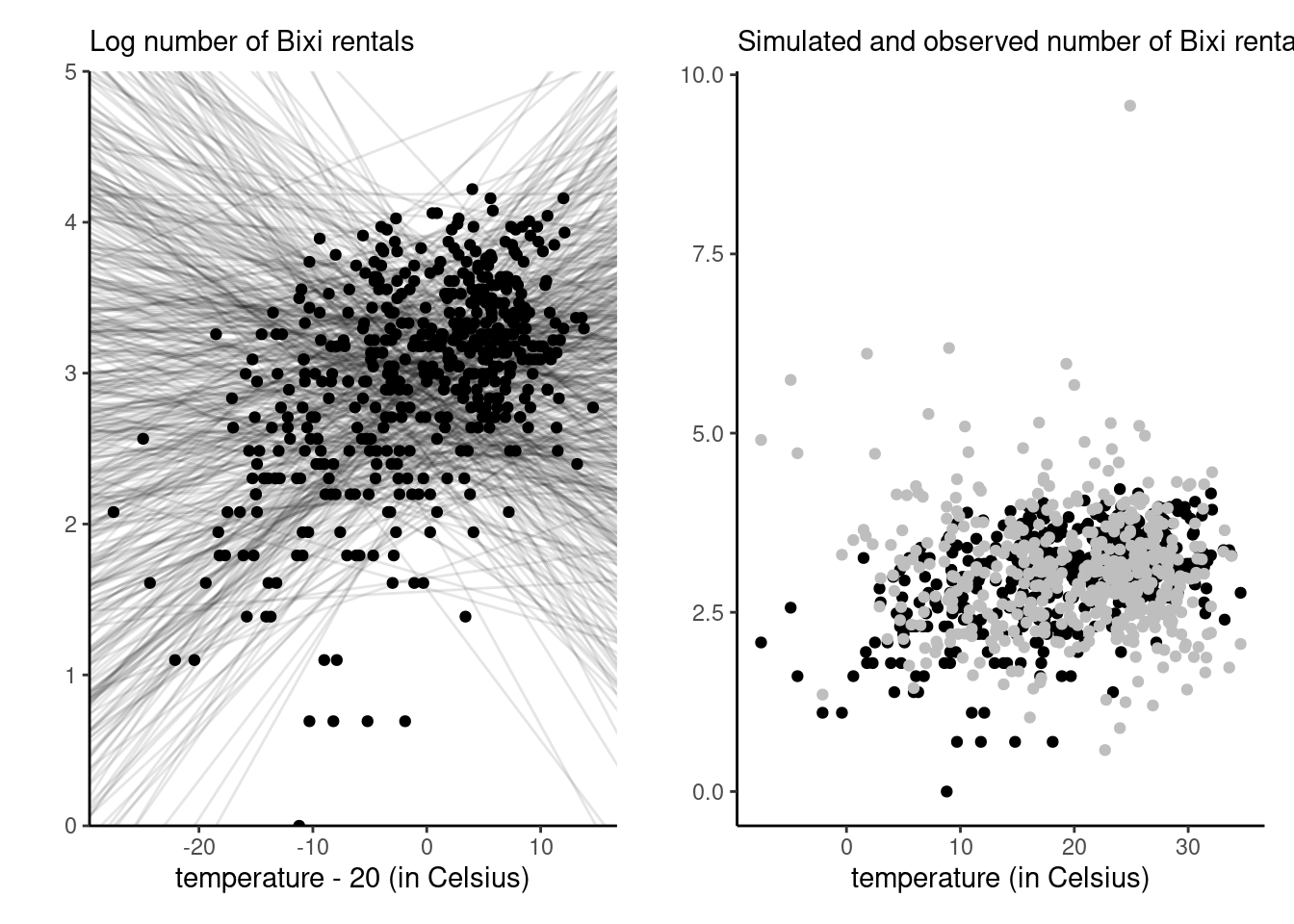
Example 3.1 Consider the daily number of Bixi bike sharing users for 2017–2019 at the Edouard Montpetit station next to HEC: we can consider a simple linear regression with log counts as a function of temperature,1 \[\log (\texttt{nusers}) \sim \mathsf{Gauss}_{+}\{\beta_0 + \beta_1 (\texttt{temp}-20), \sigma^2\}.\] The \(\beta_1\) slope measures units in degree Celsius per log number of person.
The hyperparameters depend of course on the units of the analysis, unless one standardizes response variable and explanatories: it is easier to standardize the temperature so that we consider deviations from, say 20\(^{\circ}\)C, which is not far from the observed mean in the sample. After some tuning, the independent priors \(\beta_0 \sim \mathsf{Gauss}(\overline{y}, 0.5^2),\) \(\beta_1 \sim \mathsf{Gauss}(0, 0.05^2)\) and \(\sigma \sim \mathsf{Exp}(3)\) seem to yield plausible outcomes and relationships.2

We can draw regression lines from the prior, as in the left panel of Figure 3.1: while some of the negative relationships appear unlikely after seeing the data, the curves all seem to pass somewhere in the cloud of point. By contrast, a silly prior is one that would result in all observations being above or below the regression line, or yield values that are much too large near the endpoints of the explanatory variable. Indeed, given the number of bikes for rental is limited (a docking station has only 20 bikes), it is also sensible to ensure that simulations do not return overly large numbers. The maximum number of daily users in the sample is 68, so priors that return simulations with more than 200 (rougly 5.3 on the log scale) are not that plausible. The prior predictive draws can help establish this and the right panel of Figure 3.1 shows that, expect for the lack of correlation between temperature and number of users, the simulated values from the prior predictive are plausible even if overdispersed.
3.2 Conjugate priors
In very simple models, there may exists prior densities that result in a posterior distribution of the same family. We can thus directly extract characteristics of the posterior. Conjugate priors are chosen for computational convenience and because interpretation is convenient, as the parameters of the posterior will often be some weighted average of prior and likelihood component.
Definition 3.1 (Conjugate priors) A prior density \(p(\boldsymbol{\theta})\) is conjugate for likelihood \(L(\boldsymbol{\theta}; \boldsymbol{y})\) if the product \(L(\boldsymbol{\theta}; \boldsymbol{y})p(\boldsymbol{\theta}),\) after renormalization, is of the same parametric family as the prior.
Exponential families (see Definition 1.13, including the binomial, Poisson, exponential, Gaussian distributions) admit conjugate priors.
| distribution | unknown parameter | conjugate prior |
|---|---|---|
| \(Y \sim \mathsf{expo}(\lambda)\) | \(\lambda\) | \(\lambda \sim \mathsf{gamma}(\alpha, \beta)\) |
| \(Y \sim \mathsf{Poisson}(\mu)\) | \(\mu\) | \(\mu \sim \mathsf{gamma}(\alpha, \beta)\) |
| \(Y \sim \mathsf{binom}(n, \theta)\) | \(\theta\) | \(\theta \sim \mathsf{Be}(\alpha, \beta)\) |
| \(Y \sim \mathsf{Gauss}(\mu, \sigma^2)\) | \(\mu\) | \(\mu \sim \mathsf{Gauss}(\nu, \omega^2)\) |
| \(Y \sim \mathsf{Gauss}(\mu, \sigma^2)\) | \(\sigma\) | \(\sigma^{2} \sim \mathsf{inv. gamma}(\alpha, \beta)\) |
| \(Y \sim \mathsf{Gauss}(\mu, \sigma^2)\) | \(\mu, \sigma\) | \(\mu \mid \sigma^2 \sim \mathsf{Gauss}(\nu, \omega \sigma^2),\) \(\sigma^{2} \sim \mathsf{inv. gamma}(\alpha, \beta)\) |
Example 3.2 (Conjugate prior for the binomial model) Since the density of the binomial is of the form \(p^y(1-p)^{n-y}\) and it belongs to an exponential family (Example 1.2), the beta distribution \(\mathsf{beta}(\alpha, \beta)\) with density \[f(x) \propto x^{\alpha-1} (1-x)^{\beta-1}\] is the conjugate prior.
The beta distribution is also the conjugate prior for the negative binomial, geometric and Bernoulli distributions, since their likelihoods are all proportional to that of the beta. The fact that different sampling schemes that result in proportional likelihood functions give the same inference is called likelihood principle.
Example 3.3 (Conjugate prior for the Poisson model) We saw in Example 1.3 that the Poisson distribution is an exponential family. The gamma density, \[ f(x) \propto \beta^{\alpha}/\Gamma(\alpha)x^{\alpha-1} \exp(-\beta x)\] with shape \(\alpha\) and rate \(\beta\) is the conjugate prior for the Poisson. For an \(n\)-sample of independent observations \(\mathsf{Poisson}(\mu)\) observations with \(\mu \sim \mathsf{gamma}(\alpha, \beta),\) the posterior is \(\mathsf{gamma}(\sum_{i=1}^n y_i + \alpha, \beta + n).\)
Knowing the analytic expression for the posterior can be useful for calculations of the marginal likelihood, as Example 1.13 demonstrated.
Example 3.4 (Posterior rates for A/B tests using conjugate Poisson model) Upworthy.com, a US media publisher, revolutionized headlines online advertisement by running systematic A/B tests to compare the different wording of headlines, placement and image and what catches attention the most. The Upworthy Research Archive (Matias et al. 2021) contains results for 22743 experiments, with a click through rate of 1.58% on average and a standard deviation of 1.23%. The clickability_test_id gives the unique identifier of the experiment, clicks the number of conversion out of impressions. See Section 8.5 of Alexander (2023) for more details about A/B testing and background information.
Consider an A/B test from November 23st, 2014, that compared four different headlines for a story on Sesame Street workshop with interviews of children whose parents were in jail and visiting them in prisons. The headlines tested were:
- Some Don’t Like It When He Sees His Mom. But To Him? Pure Joy. Why Keep Her From Him?
- They’re Not In Danger. They’re Right. See True Compassion From The Children Of The Incarcerated.
- Kids Have No Place In Jail … But In This Case, They Totally Deserve It.
- Going To Jail Should Be The Worst Part Of Their Life. It’s So Not. Not At All.
At first glance, the first and third headlines seem likely to lead to a curiosity gap. The wording of the second is more explicit (and searchable), whereas the first is worded as a question.
We model the conversion rate \(\lambda_i\) for each headline separately using a Poisson distribution and compare the posterior distributions for all four choices. Using a conjugate prior and selecting the parameters by moment matching yields approximately \(\alpha = 1.65\) and \(\beta = 104.44\) for the hyperparameters, setting \(\alpha/\beta = 0.0158\) and \(\alpha/\beta^2=0.0123^2\) and solving for the two unknown parameters.
| headline | impressions | clicks |
|---|---|---|
| H1 | 3060 | 49 |
| H2 | 2982 | 20 |
| H3 | 3112 | 31 |
| H4 | 3083 | 9 |
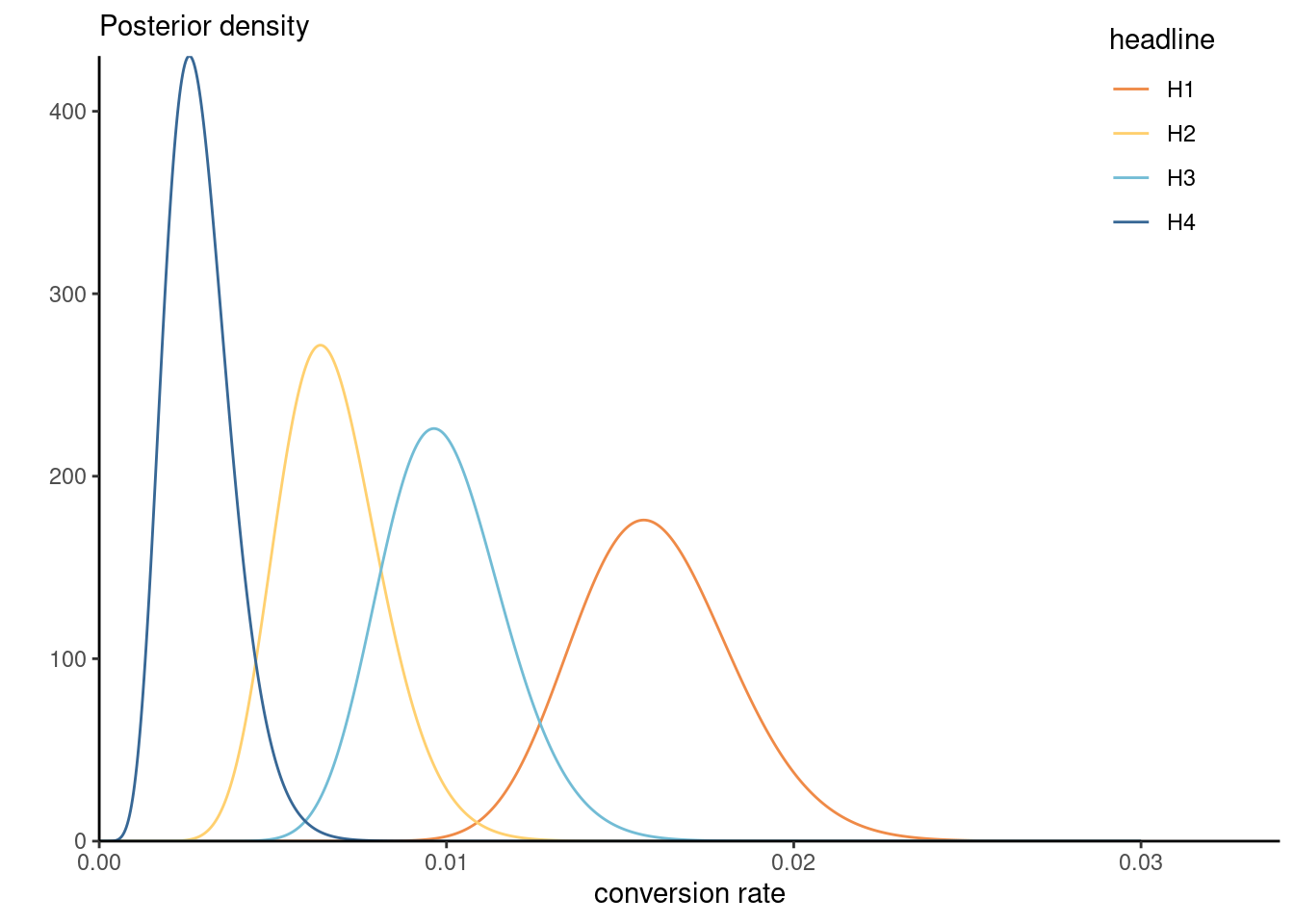
We can visualize the posterior distributions. In this context, the large sample size lead to the dominance of the likelihood contribution \(p(Y_i \mid \lambda_i) \sim \mathsf{Poisson}(n_i\lambda_i)\) relative to the prior. We can see there is virtually no overlap between different rates for headers H1 (preferred) relative to H4 (least favorable). The probability that the conversion rate for Headline 3 is higher than Headline 1 can be approximated by simulating samples from both posteriors and computing the proportion of times one is larger: we get 2% for H3 relative to H1, indicating a clear preference for the first headline H1.
Example 3.5 (Should you phrase your headline as a question?) We can also consider aggregate records for Upworthy, as Alexander (2023) did. The upworthy_question database contains a balanced sample of all headlines where at least one of the choices featured a question, with at least one alternative statement. Whether a headline contains a question or not is determined by querying for the question mark. We consider aggregated counts for all such headlines, with the question factor encoding whether there was a question, yes or no. For simplicity, we treat the number of views as fixed, but keep in mind that A/B tests are often sequential experiments with a stopping rule.3
We model first the rates using a Poisson regression; the corresponding frequentist analysis would include an offset to account for differences in views. If \(\lambda_{j}\) \((j=1, 2)\) are the average rate for each factor level (yes and no), then \(\mathsf{E}(Y_{ij}/n_{ij}) = \lambda_j.\) In the frequentist setting, we can fit a simple Poisson generalized linear regression model with an offset term and a binary variable.
data(upworthy_question, package = "hecbayes")
poismod <- glm(
clicks ~ offset(log(impressions)) + question,
family = poisson(link = "log"),
data = upworthy_question)
coef(poismod)(Intercept) questionno
-4.51264669 0.07069677 The coefficients represent the difference in log rate (multiplicative effect) relative to the baseline rate, with an increase of 6.3 percent when the headline does not contain a question. A likelihood ratio test can be performed by comparing the deviance of the null model (intercept-only), indicating strong evidence that including question leads to significatively different rates. This is rather unsurprising given the enormous sample sizes.
Consider instead a Bayesian analysis with conjugate prior: we model separately the rates of each group (question or not). Suppose we think apriori that the click-rate is on average 1%, with a standard deviation of 2%, with no difference between questions or not. For a \(\mathsf{Gamma}(\alpha, \beta)\) prior, this would translate, using moment matching, into a rate of \(\beta = 25 = \mathsf{E}_0(\lambda_j)/ \mathsf{Var}_0(\lambda_j)\) and a shape of \(\alpha = 0.25\) (\(j=1, 2\)). If \(\lambda_{j}\) is the average rate for each factor level (yes and no), then \(\mathsf{E}(Y_{ij}/n_{ij}) = \lambda_j\) so the log likelihood is proportional, as a function of \(\lambda_1\) and \(\lambda_2,\) to \[\begin{align*} \ell(\boldsymbol{\lambda}; \boldsymbol{y}, \boldsymbol{n}) \stackrel{\boldsymbol{\lambda}}{\propto} \sum_{i=1}^n \sum_{j=1}^2 y_{ij}\log \lambda_j - \lambda_jn_{ij} \end{align*}\] and we can recognize that the posterior for \(\lambda_i\) is gamma with shape \(\alpha + \sum_{i=1}^n y_{ij}\) and rate \(\beta + \sum_{i=1}^n n_{ij}.\) For inference, we thus only need to select hyperparameters and calculate the total number of clicks and impressions per group. We can then consider the posterior difference \(\lambda_1 - \lambda_2\) or, to mimic the Poisson multiplicative model, of the ratio \(\lambda_1/\lambda_2.\) The former suggests very small differences, but one must keep in mind that rates are also small. The ratio, shown in the right-hand panel of Figure 3.3, gives a more easily interpretable portrait that is in line with the frequentist analysis.
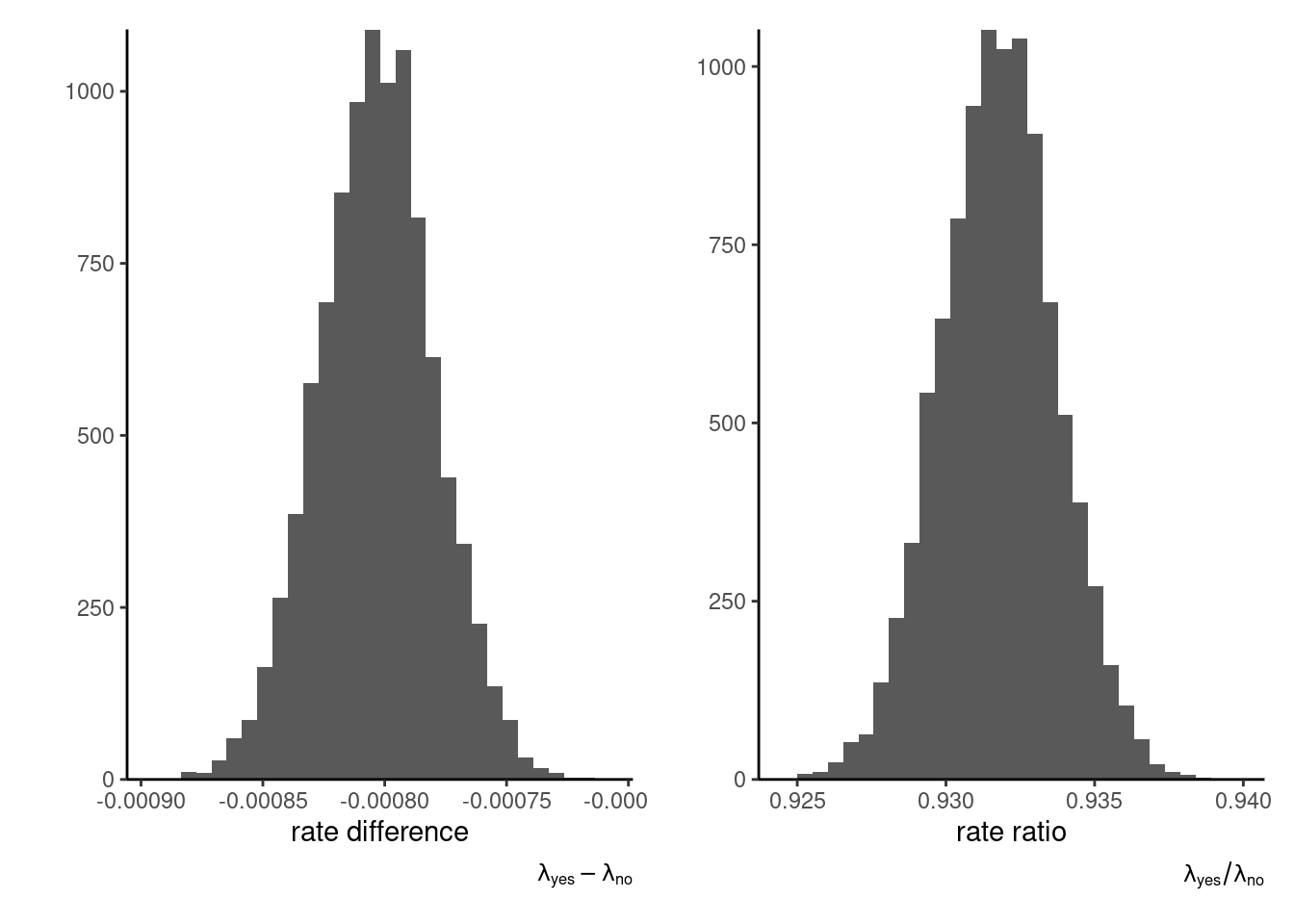
To get an approximation to the posterior mean of the ratio \(\lambda_1/\lambda_2,\) it suffices to draw independent observations from their respective posterior, compute the ratio and take the sample mean of those draws. We can see that the sampling distribution of the ratio is nearly symmetrical, so we can expect Wald intervals to perform well should one be interested in building confidence intervals. This is however hardly surprising given the sample size at play.
Example 3.6 (Conjugate prior for Gaussian mean with known variance) Consider an \(n\) simple random sample of independent and identically distributed Gaussian variables with mean \(\mu\) and standard deviation \(\sigma,\) denoted \(Y_i \sim \mathsf{Gauss}(\mu, \sigma^2).\) We pick a Gaussian prior for the location parameter, \(\mu \sim \mathsf{Gauss}(\nu, \tau^2)\) where we assume \(\nu, \tau\) are fixed hyperparameter values. For now, we consider only inference for the conditional marginal posterior \(p(\mu \mid \boldsymbol{y}, \sigma)\): discarding any term that is not a function of \(\mu,\) the conditional posterior is \[\begin{align*} p(\mu \mid \sigma, \boldsymbol{y}) &\propto \exp\left\{ -\frac{1}{2\sigma^2}\sum_{i=1}^n (y_{i}-\mu)^2\right\} \exp\left\{-\frac{1}{2\tau^2}(\mu - \nu)^2\right\} \\&\propto \exp\left\{\left(\frac{\sum_{i=1}^n y_{i}}{\sigma^2} + \frac{\nu}{\tau^2}\right)\mu - \left( \frac{n}{2\sigma^2} +\frac{1}{2\tau^2}\right)\mu^2\right\}. \end{align*}\] The log of the posterior density conditional on \(\sigma\) is quadratic in \(\mu,\) it must be a Gaussian distribution truncated over the positive half line. This can be seen by completing the square in \(\mu,\) or by comparing this expression to the density of \(\mathsf{Gauss}(\mu, \sigma^2),\) \[\begin{align*} f(x; \mu, \sigma) \stackrel{\mu}{\propto} \exp\left(-\frac{1}{2 \sigma^2}\mu^2 + \frac{x}{\sigma^2}\mu\right) \end{align*}\] we can deduce by matching mean and variance that the conditional posterior \(p(\mu \mid \sigma)\) is Gaussian with reciprocal variance (precision) \(n/\sigma^2 + 1/\tau^2\) and mean \((n\overline{y}\tau^2 + \nu \sigma^2)/(n\tau^2 + \sigma^2).\) The precision is an average of that of the prior and data, but assigns more weight to the latter, which increases linearly with the sample size \(n.\) Likewise, the posterior mean is a weighted average of prior and sample mean, with weights proportional to the relative precision.
The exponential family is quite large; Fink (1997) A Compendium of Conjugate Priors gives multiple examples of conjugate priors and work out parameter values.
In general, unless the sample size is small and we want to add expert opinion, we may wish to pick an uninformative prior, i.e., one that does not impact much the outcome. For conjugate models, one can often show that the relative weight of prior parameters (relative to the random sample likelihood contribution) becomes negligible by investigating their relative weights.
3.3 Uninformative priors
Definition 3.2 (Proper prior) We call a prior function proper if it’s integral is finite over the parameter space; such prior function automatically leads to a valid posterior. A prior over \(\boldsymbol{\Theta}\) is improper if \(\int_{\boldsymbol{\Theta}} p(\boldsymbol{\theta}) \mathrm{d} \boldsymbol{\theta} = \infty.\)
The best example of proper priors arise from probability density function. We can still employ this rule for improper priors: for example, taking \(\alpha, \beta \to 0\) in the beta prior leads to a prior proportional to \(x^{-1}(1-x)^{-1},\) the integral of which diverges on the unit interval \([0,1].\) However, as long as the number of success and the number of failures is larger than 1, meaning \(k \geq 1, n-k \geq 1,\) the posterior distribution would be proper, i.e., integrable. To find the posterior, normalizing constants are also superfluous.
Many uninformative priors are flat, or proportional to a uniform on some subset of the real line and therefore improper. It may be superficially tempting to set a uniform prior on a large range to ensure posterior property, but the major problem is that a flat prior may be informative in a different parametrization, as the following example suggests.
Gelman et al. (2013) uses the following taxonomy for various levels of prior information:
- uninformative priors are generally flat or uniform priors with \(p(\beta) \propto 1.\)
- vague priors are typically nearly flat even if proper, e.g., \(\beta \sim \mathsf{Gauss}(0, 100),\)
- weakly informative priors provide little constraints \(\beta \sim \mathsf{Gauss}(0, 10),\) and
- informative prior are typically application-specific, but constrain the ranges.
Uninformative and vague priors are generally not recommended unless they are known to give valid posterior inference and the amount of information from the likelihood is high.
Example 3.7 (Transformation of flat prior for scales) Consider the parameter \(\log(\tau) \in \mathbb{R}\) and the prior \(p( \log \tau) \propto 1.\) If we reparametrize the model in terms of \(\tau,\) the new prior (including the Jacobian of the transformation) is \(\tau^{-1}\)
Some priors are standard and widely used. In location scale families with location \(\nu\) and scale \(\tau,\) the density is such that \[\begin{align*} f(x; \nu, \tau) = \frac{1}{\tau} f\left(\frac{x - \nu}{\tau}\right), \qquad \nu \in \mathbb{R}, \tau >0. \end{align*}\] We thus wish to have a prior so that \(p(\tau) = c^{-1}p(\tau/c)\) for any scaling \(c>0,\) whence it follows that \(p(\tau) \propto \tau^{-1},\) which is uniform on the log scale.
The priors \(p(\nu) \propto 1\) and \(p(\tau) \propto \tau^{-1}\) are both improper but lead to location and scale invariance, hence that the result is the same regardless of the units of measurement.
One criticism of the Bayesian approach is the arbitrariness of prior functions. However, the role of the prior is often negligible in large samples (consider for example the posterior of exponential families with conjugate priors). Moreover, the likelihood is also chosen for convenience, and arguably has a bigger influence on the conclusion. Data fitted using a linear regression model seldom follow Gaussian distributions conditionally, in the same way that the linearity is a convenience (and first order approximation).
Definition 3.3 (Jeffrey’s prior) In single parameter models, taking a prior function for \(\theta\) proportional to the square root of the determinant of the information matrix, \(p(\theta) \propto |\imath(\theta)|^{1/2}\) yields a prior that is invariant to reparametrization, so that inferences conducted in different parametrizations are equivalent.4
To see this, consider a bijective transformation \(\theta \mapsto \vartheta.\) Under the reparametrized model and suitable regularity conditions5, the chain rule implies that \[\begin{align*} i(\vartheta) &= - \mathsf{E} \left(\frac{\partial^2 \ell(\vartheta)}{\partial^2 \vartheta}\right) \\&= - \mathsf{E}\left(\frac{\partial^2 \ell(\theta)}{\partial \theta^2}\right) \left( \frac{\mathrm{d} \theta}{\mathrm{d} \vartheta} \right)^2 + \mathsf{E}\left(\frac{\partial \ell(\theta)}{\partial \theta}\right) \frac{\mathrm{d}^2 \theta}{\mathrm{d} \vartheta^2} \end{align*}\] Since the score has mean zero, \(\mathsf{E}\left\{\partial \ell(\theta)/\partial \theta\right\}=0\) and the rightmost term vanishes. We can thus relate the Fisher information in both parametrizations, with \[\begin{align*} \imath^{1/2}(\vartheta) = \imath^{1/2}(\theta) \left| \frac{\mathrm{d} \theta}{\mathrm{d} \vartheta} \right|, \end{align*}\] implying invariance.
In multiparameter models, the system isn’t invariant to reparametrization if we consider the determinant of the Fisher information.
Example 3.8 (Jeffrey’s prior for the binomial distribution) Consider the binomial distribution \(\mathsf{Bin}(1, \theta)\) with density \(f(y; \theta) \propto \theta^y(1-\theta)^{1-y}\mathbf{1}_{\theta \in [0,1]}.\) The negative of the second derivative of the log likelihood with respect to \(p\) is \[\jmath(\theta) = - \partial^2 \ell(\theta; y) / \partial \theta^2 = y/\theta^2 + (1-y)/(1-\theta)^2\] and since \(\mathsf{E}(Y)=\theta,\) the Fisher information is \[\imath(\vartheta) = \mathsf{E}\{\jmath(\theta)\}=1/\theta + 1/(1-\theta) = 1/\{\theta(1-\theta)\}\] Jeffrey’s prior is thus \(p(\theta) \propto \theta^{-1/2}(1-\theta)^{-1/2},\) a conjugate Beta prior \(\mathsf{beta}(0.5,0.5).\)
Exercise 3.1 (Jeffrey’s prior for the normal distribution) Check that for the Gaussian distribution \(\mathsf{Gauss}(\mu, \sigma^2),\) the Jeffrey’s prior obtained by treating each parameter as fixed in turn, are \(p(\mu) \propto 1\) and \(p(\sigma) \propto 1/\sigma,\) which also correspond to the default uninformative priors for location-scale families.
Example 3.9 (Jeffrey’s prior for the Poisson distribution) The Poisson distribution with \(\ell(\lambda) \propto -\lambda + y\log \lambda,\) with second derivative \(-\partial^2 \ell(\lambda)/\partial \lambda^2 = y/\lambda^2.\) Since the mean of the Poisson distribution is \(\lambda,\) the Fisher information is \(\imath(\lambda) = \lambda^{-1}\) and Jeffrey’s prior is \(\lambda^{-1/2}.\)
3.4 Priors for regression models
Regression models often feature Gaussian priors on the mean coefficients \(\boldsymbol{\beta},\) typically chosen to be vague with large variance. Below are some alternatives, many of which aim to enforce shrinkage towards zero, or sparsity.
Proposition 3.1 (Zellner’s \(g\) prior) Consider an ordinary linear regression model for \(\boldsymbol{Y} \sim \mathsf{Gauss}_n(\beta_0\mathbf{1}_n + \mathbf{X}\boldsymbol{\beta}, \sigma^2 \mathbf{I}_n),\) with intercept \(\beta_0\) and mean coefficient vector \(\boldsymbol{\beta} = (\beta_1, \ldots, \beta_p)^\top\) associated to the model matrix \(\mathbf{X}.\) Zellner (1986)’s \(g\) prior consists in letting \(\boldsymbol{\beta} \sim \mathsf{Gauss}_p\{\boldsymbol{0}_p, g \sigma^2(\mathbf{X}^\top\mathbf{X})^{-1}\},\) where \(g>0\) is a constant.
The ordinary least square estimator of the mean coefficients satisfies under regularity conditions on the model matrix \(\widehat{\boldsymbol{\beta}} \sim \mathsf{Gauss}_p\{\boldsymbol{\beta}, \sigma^2(\mathbf{X}^\top\mathbf{X})^{-1}\}\) for Gaussian data, whence we get the closed-form conditional distributions \[\begin{align*} \beta_0 \mid \sigma^2, \boldsymbol{Y} &\sim \mathsf{Gauss}(\overline{y}, \sigma^2/n)\\ \boldsymbol{\beta} \mid \beta_0, \sigma^2, \boldsymbol{Y} & \sim \mathsf{Gauss}_p\left\{\frac{g}{g+1} \widehat{\boldsymbol{\beta}}, \frac{g}{g+1}\sigma^2 (\mathbf{X}^\top\mathbf{X})^{-1}\right\} \end{align*}\] where \(\overline{y} = \boldsymbol{y}^\top\mathbf{1}_n/n\) is the sample mean of the observed response vector. We can interpret \(g>0\) as a prior weight, with the posterior conditional mean giving weight of \(n/g\) to “phantom (prior) observations” with mean zero, relative to the \(n\) observations in the observed sample: the ratio \(g/(g+1)\) is called shrinkage factor.
By virtue of Proposition 1.6, the prior is also closed under conditioning, which is useful for model comparison using Bayes factors. Consider a partition \(\boldsymbol{\beta} = (\boldsymbol{\beta}_1^\top, \boldsymbol{\beta}_2^\top)^\top\) of the mean coefficients and similarly the block of columns from the model matrix, say \(\mathbf{X} = [\mathbf{X}_1\; \mathbf{X}_2]\) for blocks of size \(k\) and \(p-k.\) If we remove \(p-k\) regressors from the model setting \(\boldsymbol{\beta}_2=0,\) then the conditional is \[\boldsymbol{\beta}_{1} \mid \boldsymbol{\beta}_2=\boldsymbol{0}_{p-k} \sim \mathsf{Gauss}_k\{\boldsymbol{0}_k, g\sigma^2 (\mathbf{X}_1^\top\mathbf{X}_1)^{-1}\},\] which is the \(g\) prior for the submodel in which we omit the columns corresponding to \(\mathbf{X}_2.\)
3.5 Informative priors
One strength of the Bayesian approach is the capability of incorporating expert and domain-based knowledge through priors. Often, these will take the form of moment constraints, so one common way to derive a prior is to perform moment matching to related elicited quantities with moments of the prior distribution. It may be easier to set priors on a different scale than those of the observations, as Example 3.10 demonstrates.
Example 3.10 (Gamma quantile difference priors for extreme value distributions) The generalized extreme value distribution arises as the limiting distribution for the maximum of \(m\) independent observations from some common distribution \(F.\) The \(\mathsf{GEV}(\mu, \sigma, \xi)\) distribution is a location-scale with distribution function \[\begin{align*} F(x) = \exp\left[ - \left\{1+\xi(x-\mu)/\sigma\right\}^{-1/\xi}_{+}\right] \end{align*}\] where \(x_{+} = \max\{0, x\}.\)
Inverting the distribution function yields the quantile function \[\begin{align*} Q(p) \mu + \sigma \frac{(-\log p)^{-\xi}-1}{\xi} \end{align*}\]
In environmental data, we often model annual maximum. Engineering designs are often specified in terms of the \(k\)-year return levels, defined as the quantile of the annual maximum exceeded with probability \(1/k\) in any given year. Using a \(\mathsf{GEV}\) for annual maximum, Coles and Tawn (1996) proposed modelling annual daily rainfall and specifying a prior on the quantile scale \(q_1 < q_2 < q_3\) for tail probabilities \(p_1> p_2 > p_3.\) To deal with the ordering constraints, gamma priors are imposed on the differences
- \(q_1 - o \sim \mathsf{gamma}(\alpha_1, \beta_1),\)
- \(q_2 - q_1 \sim \mathsf{gamma}(\alpha_2, \beta_2)\) and
- \(q_3-q_2 \sim \mathsf{gamma}(\alpha_3, \beta_3),\)
where \(o\) is the lower bound of the support. The prior is thus of the form \[\begin{align*} p(\boldsymbol{q}) \propto q_1^{\alpha_1-1}\exp(-\beta_1 q_1) \prod_{i=2}^3 (q_i-q_{i-1})^{\alpha_i-1} \exp\{\beta_i(q_i-q_{i-1})\}. \end{align*}\] where \(0 \leq q_1 \leq q_2 \leq q_3.\) The fact that these quantities refer to moments or risk estimates which practitioners often must compute as part of regulatory requirements makes it easier to specify sensible values for hyperparameters.
Example 3.11 (Priors in extreme value theory) The generalized extreme value distribution obtained as the limit of maximum of blocks of size \(m\) when suitably normalizes is a location-scale family with a shape parameter \(\xi \in \mathbb{R}\). The latter describes the heavyness of the tail, with negative values corresponding to approximation by bounded upper tail distributions (such as the beta), \(\xi=0\) to exponential tail decay and \(\xi>0\) to polynomial tails, with finite moments of order \(1/\xi\). For example, the Cauchy or Student-\(t\) distribution with one degree of freedom has infinite first moment and \(\xi=1\).
In practice, the maximum likelihood estimators do not exist if \(\xi < -1\) as the model is nonregular (Smith 1985), and the cumulant of order \(k\) exists only if \(\xi > -1/k\); the Fisher information matrix exists only when \(\xi > -1/2\). Thus, informative priors that restrict the range of the shape, may be useful as in environmental applications the shapes would be in the vicinity of zero. Martins and Stedinger (2000) proposed a prior of the form \[\begin{align*} p(\xi) =\frac{(0.5+\xi)^{p-1}(0.5-\xi)^{q-1}}{\mathrm{beta}(p,q)}, \qquad \xi \in [-0.5, 0.5] \end{align*}\] a shifted \(\mathsf{beta}(p,q)\) prior.
On the contrary, the maximal data information (MDI) prior (Zellner 1971) is defined in terms of entropy, \[p(\boldsymbol{\theta}) = \exp \mathsf{E}\{\log f(Y \mid \boldsymbol{\theta})\}.\] It is an objective prior that reflects little about the parameter and leads to inferences that have good frequentist property.
For the generalized Pareto distribution, \(p(\xi) \propto \exp(-\xi)\). In this particular case, however, it is improper without modification since \(\lim_{\xi \to -\infty} \exp(-\xi) = \infty\), and the prior density increases without bound as \(\xi\) becomes smaller.
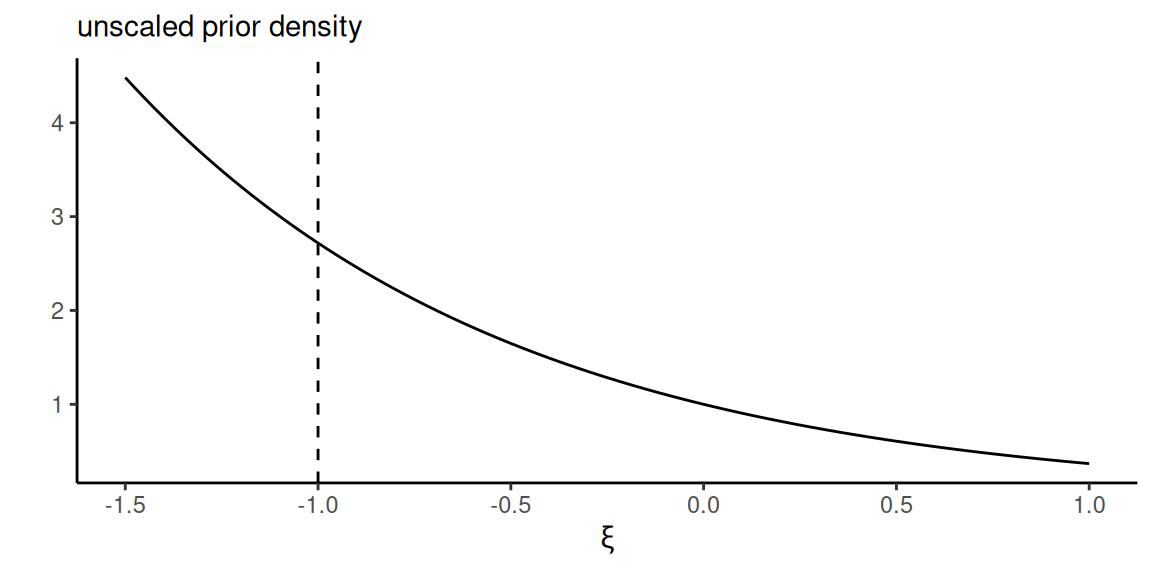
If we restrict the range of the MDI prior \(p(\xi)\) to \(\xi \geq -1\), then \(p(\xi + 1) \sim \mathsf{expo}(1)\) and the resulting posterior is proper Zhang and Shaby (2023). While being “objective”, it is perhaps not much suitable as it puts mass towards lower values of the shape, an undesirable feature.
What would you do if we you had prior information from different sources? One way to combine these is through a mixture: given \(M\) different prior distributions \(p_m(\boldsymbol{\theta}),\) we can assign each a positive weight \(w_m\) to form a mixture of experts prior through the linear combination \[ p(\boldsymbol{\theta}) \propto \sum_{m=1}^M w_m p_m(\boldsymbol{\theta})\]
Proposition 3.2 (Penalized complexity priors) Oftentimes, there will be a natural family of prior density to impose on some model component, \(p(\boldsymbol{\theta} \mid \zeta),\) with hyperparameter \(\zeta.\) The flexibility of the underlying construction leads itself to overfitting. Penalized complexity priors (Simpson et al. 2017) aim to palliate this by penalizing models far away from a simple baseline model, which correspond to a fixed value \(\zeta_0.\) The prior will favour the simpler parsimonious model the more prior mass one places on \(\zeta_0,\) which is in line with Occam’s razor principle.
To construct a penalized-complexity prior, we compute the Kullback–Leibler divergence (Simpson et al. 2017) or the Wasserstein distance (Bolin, Simas, and Xiong 2023) between the model \(p_\zeta \equiv p(\boldsymbol{\theta} \mid \zeta)\) relative to the baseline with \(\zeta_0,\) \(p_0 \equiv p(\boldsymbol{\theta} \mid \zeta_0);\) the distance between the prior densities is then set to \(d(\zeta) = \{2\mathsf{KL}(p_\zeta \mid\mid p_0)\}^{1/2},\) where the Kullback–Leibler divergence is \[\begin{align*} \mathsf{KL}(p_\zeta \Vert\, p_0)=\int p_\zeta \log\left(\frac{p_\zeta}{p_0}\right) \mathrm{d} \boldsymbol{\theta}. \end{align*}\] The divergence is zero at the model with \(\zeta_0.\) The PC prior then constructs an exponential prior on the distance scale, which after back-transformation gives \(p(\zeta \mid \lambda) = \lambda\exp(-\lambda d(\zeta)) \left| {\partial d(\zeta)}/{\partial \zeta}\right|.\) To choose \(\lambda,\) the authors recommend elicitation of a pair \((Q_\zeta, \alpha)\), where \(Q_\zeta\) is the quantile at level \(1-\alpha\), such that \(\Pr(\lambda > Q_\zeta)=\alpha.\)
The construction of Wasserstein complexity priors (Bolin, Simas, and Xiong 2023) is more involved, but those priors are also parametrization-invariant and well-defined even when the Kullback–Leibler divergence limit does not exist.
Example 3.12 (Penalized complexity prior for random effects models) Bolin, Simas, and Xiong (2023) consider a Gaussian prior for independent and identically random effects \(\boldsymbol{\alpha},\) of the form \(\alpha_j \mid \zeta \sim \mathsf{Gauss}(0, \zeta^2)\) where \(\zeta_0=0\) corresponds to the absence of random subject-variability. The penalized complexity prior for the scale \(\zeta\) is then an exponential with rate \(\lambda,\) with density \[p(\zeta \mid \lambda) = \lambda \exp(-\lambda \zeta).\]
We can elicit a high quantile \(Q_\zeta\) at tail probability \(\alpha\) for the standard deviation parameter \(\zeta\) and set \(\lambda = -\ln(\alpha/Q_\zeta)\).
Example 3.13 (Penalized complexity prior for autoregressive model of order 1) Sørbye and Rue (2017) derive penalized complexity prior for the Gaussian stationary AR(1) model with autoregressive parameter \(\phi \in (-1,1),\) where \(Y_t \mid Y_{t-1}, \phi, \sigma^2 \sim \mathsf{Gauss}(\phi Y_{t-1}, \sigma^2).\) There are two based models that could be of interest: one with \(\phi=0,\) corresponding to a memoryless model with no autocorrelation, and a static mean \(\phi=1\) for no change in time; note that the latter is not stationary. For the former \((\phi=0)\), the penalized complexity prior is \[\begin{align*} p(\phi \mid \lambda) = \frac{\lambda}{2} \exp\left[-\lambda \left\{-\ln(1-\phi^2)\right\}^{1/2}\right] \frac{|\phi|}{(1-\phi^2)\left\{-\ln(1-\phi^2)\right\}^{1/2}}. \end{align*}\] One can set \(\lambda\) by considering plausible values by relating the parameter to the variance of the one-step ahead forecast error.
Remark 3.1 (Variance parameters in hierarchical models). Gaussian components are widespread: not only for linear regression models, but more generally for the specification of random effects that capture group-specific effects, residuals spatial or temporal variability. In the Bayesian paradigm, there is no difference between fixed effects \(\boldsymbol{\beta}\) and the random effect parameters: both are random quantities that get assigned priors, but we will treat these priors differently.
The reason why we would like to use a penalized complexity prior for a random effect, say \(\alpha_j \sim \mathsf{Gauss}(0, \zeta^2),\) is because we don’t know a prior if there is variability between groups. The inverse gamma prior for \(\zeta,\) \(\zeta \sim \mathsf{InvGamma}(\epsilon, \epsilon)\) does not have a mode at zero unless it is improper with \(\epsilon \to 0.\) Generally, we want our prior for the variance to have significant probability density at the null \(\zeta=0.\) The penalized complexity prior is not the only sensible choice. Posterior inference is unfortunately sensitive to the value of \(\epsilon\) in hierarchical models when the random effect variance is close to zero, and more so when there are few levels for the groups since the relative weight of the prior relative to that of the likelihood contribution is then large.
Example 3.14 (Student-t prior for variance components) Gelman (2006) recommends a Student-\(t\) distribution truncated below at \(0,\) with low degrees of freedom. The rationale for this choice comes from the simple two level model with \(n_j\) independent in each group \(j=1, \ldots, J\): for observation \(i\) in group \(j,\) \[\begin{align*} Y_{ij} &\sim \mathsf{Gauss}(\mu + \alpha_j, \sigma^2),\\ \alpha_j &\sim \mathsf{Gauss}(0, \tau^2_\alpha), \end{align*}\] The conditionally conjugate prior \(p(\tau \mid \boldsymbol{\alpha}, \mu, \sigma)\) is inverse gamma. Standard inference with this parametrization is however complicated, because there is strong dependence between parameters.
To reduce this dependence, one can add a parameter, taking \(\alpha_j = \xi \eta_j\) and \(\tau_\alpha=|\xi|\tau_{\eta}\); the model is now overparametrized. Suppose \(\eta_j \sim \mathsf{Gauss}(0, \tau^2_\eta)\) and consider the likelihood conditional on \(\mu, \eta_j\): we have that \((y_{ij} - \mu)/\eta_j \sim \mathsf{Gauss}(\xi, \sigma^2/\eta_j)\) so conditionally conjugate priors for \(\xi\) and \(\tau_\eta\) are respectively Gaussian and inverse gamma. This translates into a prior distribution for \(\tau_\alpha\) which is that of the absolute value of a noncentral Student-\(t\) with location, scale and degrees of freedom \(\nu.\) If we set the location to zero, the prior puts high mass at the origin, but is heavy tailed with polynomial decay. We recommend to set degrees of freedom so that the variance is heavy-tailed, e.g., \(\nu=3.\) While this prior is not conjugate, it compares favorably to the \(\mathsf{inv. gamma}(\epsilon, \epsilon).\)
- Priors are distributions for the parameters. In multi-parameter models, they can be specified through a joint distribution or assumed independent apriori (which does not translate into independence a posteriori).
- Priors are not invariant to reparametrization, except when they are constructed with this property (e.g., Jeffrey’s prior or penalized-complexity priors).
- Improper priors may lead to improper posterior.
- Priors that restrict the domain of \(\boldsymbol{\theta}\) will also restrict the posterior. These are useful to avoid regions that are implausible or impossible.
- Physical knowledge of the system can be helpful to specify sensible values of the prior through moment matching.
- Conjugate priors facilitate derivations, but are mostly chosen for convenience.
- Generally, the prior has constant weight \(\mathrm{O}(1)\), relative to \(\mathrm{O}(n)\) for the likelihood. The posterior is thus dominated in most circumstances by the likelihood.
- We can compute the prior to posterior gain by comparing their density (if the prior is proper).
- For many (conjugate) priors, we can view some function of the parameter as given a prior number of observations (in Gaussian models, binomial, gamma, etc.)
- Informative priors can be used to specify expert knowledge about the system. This will impact the posterior, but often in a sensible manner, thereby regularizing or improving posterior inference.
If counts are Poisson, then the log transform is variance stabilizing.↩︎
One can object to the prior parameters depending on the data, but an alternative would be to model centered data \(y-\overline{y},\) in which case the prior for the intercept parameter \(\beta_0\) would be zero.↩︎
The stopping rule means that data stops being collected once there is enough evidence to determine if an option is more suitable, or if a predetermined number of views has been reached.↩︎
The Fisher information is linear in the sample size for independent and identically distributed data so we can derive the result for \(n=1\) without loss of generality.↩︎
Using Bartlett’s identity; Fisher consistency can be established using the dominated convergence theorem.↩︎