Exercises 2
You consider the waiting times between buses coming to HEC. Your bus line has frequent buses, but you decide to check the frequency. From your prior experience, you know that measured waiting times range between 3 and 15 minutes. You collect data over the two first week of classes and get an average of 8 minutes based on 10 observations.
For modelling, we consider data to arise an independent and identically distributed sample from an exponential distribution with rate \(\lambda>0,\) with associated density \(f(x) = \lambda \exp(-\lambda x).\)
Exercise 2.1
Compute the marginal likelihood when the prior for \(\lambda\) is
- an exponential distribution with rate \(\kappa>0,\) with prior density \(p(\lambda) = \kappa \exp(-\lambda\kappa)\);
- same, but truncated above at 1, so the density is \(p(\lambda) = \kappa \exp(-\lambda\kappa)\mathrm{I}\{\lambda \leq 1\}\); the indicator function \(\mathrm{I}(\cdot)\) equals one if the condition is true and zero otherwise.
- \(\lambda \sim \mathsf{Ga}(\alpha, \beta),\) a gamma distribution with shape \(\alpha>0\) and rate \(\beta>0,\) with prior density \(p(\lambda) = \beta^\alpha\lambda^{\alpha-1}\exp(-\beta \lambda)/\Gamma(\alpha).\)
Deduce that, in all cases above and up to truncation, the posterior distribution is a gamma distribution.
Exercise 2.2
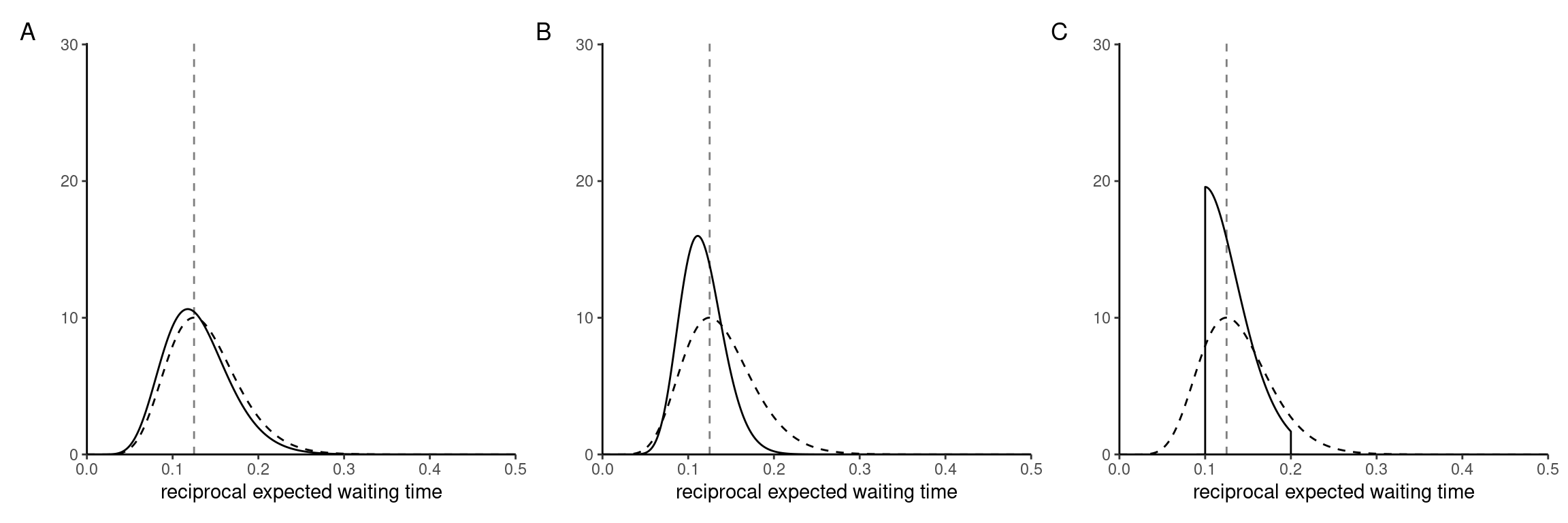
Consider the following priors for the reciprocal expected waiting time, \(\lambda.\)
- a gamma with rate \(\beta=100\) and shape \(\alpha = 10\)
- an exponential with rate \(5\)
- a uniform prior on the unit interval \([5,10]\) for \(1/\lambda\)
Associate each plot of the posterior with each of the priors. Which one seems most suitable for modelling?
Explain what would happen to the posterior curve if we increased the sample size.

Exercice 2.3
The purpose of this exercise is to show that even one-dimensional numerical integration requires some care. Consider a half Cauchy prior over the positive half line, with density \[f(x) = 2\pi^{-1}(1+x^2)^{-1}\mathrm{I}(x \geq 0).\] Using a grid approximation in increments of 0.01, evaluate the unnormalized posterior density from 0 until 30 minutes\(^{-1}.\) Compare this approximation with that of quadrature methods (e.g., via integrate in R) and return the corresponding estimates of the normalizing constant. Indication: check the values and make sure the output is sensical. Modify the integrand if necessary.
Plot the posterior distribution of \(1/\lambda,\) the average waiting time.
Exercice 2.4
Consider \(\lambda \sim \mathsf{Ga}(\alpha = 1.4, \beta=0.2).\)
- Return the posterior mean, posterior median and maximum a posteriori (MAP).
- Return the 89% equitailed percentile credible interval.
- Return the 50% highest posterior density (HPD) interval (harder). Hint: the
hdifunction from pacakgeHDIntervalmay be useful for this.
Next, draw 1000 observations from the posterior predictive distribution and plot a histogram of the latter. Compare it to the exponential distribution of observations.
Would the posterior predictive change if you gathered more data? Justify your answer and explain how it would change, if at all.