Solution 10

Exercise 10.1

Suppose that \(p(\boldsymbol{\theta})\) is a density with \(\boldsymbol{\theta} \in \mathbb{R}^d\) and that we consider a Gaussian approximation \(q(\boldsymbol{\theta})\) with mean \(\boldsymbol{\mu}\) and covariance matrix \(\boldsymbol{\Sigma}\). Show that the parameters that minimize the Kullback–Leibler \(\mathsf{KL}\{p(\boldsymbol{\theta} \parallel q(\boldsymbol{\theta})\}\) are the expectation and variance under \(p(\boldsymbol{\theta})\).1

Solution. Refer to the Matrix cookbook

Consider \(g \equiv \phi_d(\cdot; \boldsymbol{\mu},\boldsymbol{\Sigma})\) a Gaussian density and \(p(\boldsymbol{\theta})\) the target. Optimization of the parameters of \(g\) can be performed by differentiation of the target. The Kullback–Leibler divergence involves two terms: the negative entropy, which is constant, and the expected value of log density, so \[\begin{align*} \mathsf{KL}(p \parallel g) \stackrel{\boldsymbol{\mu}, \boldsymbol{\Sigma}}{\propto} -\frac{1}{2} \mathsf{E}_{p}\left\{ (\boldsymbol{\theta}-\boldsymbol{\mu})^\top\boldsymbol{\Sigma}^{-1}(\boldsymbol{\theta}-\boldsymbol{\mu})\right\} - \frac{1}{2} \log |\boldsymbol{\Sigma}| \end{align*}\] Taking gradients (formulas 57 and 61 of the Matrix Cookbook) and interchanging the order of integration and differentiation, assuming that the first two moments of \(p(\boldsymbol{\theta})\) exists, gives \[\begin{align*} \frac{\partial}{\partial \boldsymbol{\mu}} \mathsf{KL}(p \parallel g) &= \mathsf{E}_{p}\left\{(\boldsymbol{\theta}-\boldsymbol{\mu})^\top\right\}\boldsymbol{\Sigma}^{-1} \\ \frac{\partial}{\partial \boldsymbol{\Sigma}} \mathsf{KL}(p \parallel g) &= \frac{1}{2} \boldsymbol{\Sigma}^{-1} \mathsf{E}_{p}\left\{(\boldsymbol{\theta}-\boldsymbol{\mu})(\boldsymbol{\theta}-\boldsymbol{\mu})^\top\right\}\boldsymbol{\Sigma}^{-1} - \frac{1}{2}\boldsymbol{\Sigma}^{-1} \end{align*}\] Equating these to zero yields \(\mathsf{E}_p(\boldsymbol{\theta}) = \boldsymbol{\mu}\) and \(\mathsf{E}_p\left\{(\boldsymbol{\theta}-\boldsymbol{\mu})(\boldsymbol{\theta}-\boldsymbol{\mu})^\top\right\} = \boldsymbol{\Sigma}\) provided \(\boldsymbol{\Sigma}\) is invertible.

Exercise 10.2

Consider a finite mixture model of \(K\) univariate Gaussian \(\mathsf{Gauss}(\mu_k, \tau_k^{-1})\) with \(K\) fixed, whose density is \[\begin{align*} \sum_{k=1}^{K} w_k \left(\frac{\tau_k}{2\pi}\right)^{1/2}\exp \left\{-\frac{\tau_k}{2}(y_i-\mu_k)^2\right\} \end{align*}\] where \(\boldsymbol{w} \in \mathbb{S}_{K-1}\) are positive weights that sum to one, meaning \(w_1 + \cdots + w_K=1.\) We use conjugate priors \(\mu_k \sim \mathsf{Gauss}(0, 100)\), \(\tau_k \sim \mathsf{Gamma}(a, b)\) for \(k=1, \ldots, K\) and \(\boldsymbol{w} \sim \mathsf{Dirichlet}(\alpha)\) for \(a, b, \alpha>0\) fixed hyperparameter values.

To help with inference, we introduce auxiliary variables \(\boldsymbol{U}_1, \ldots, \boldsymbol{U}_n\) where \(\boldsymbol{U}_i \sim \mathsf{multinom}(1, \boldsymbol{w})\) that indicates which cluster component the model belongs to, and \(w_k = \Pr(U_{ik}=1).\)

The parameters and latent variables for the posterior of interest are \(\boldsymbol{\mu}, \boldsymbol{\tau}, \boldsymbol{w}\) and \(\boldsymbol{U}.\) Consider a factorized decomposition in which each component is independent of the others, \(g_{\boldsymbol{w}}(\boldsymbol{w})g_{\boldsymbol{\mu}}(\boldsymbol{\mu})g_{\boldsymbol{\tau}}(\boldsymbol{\tau}) g_{\boldsymbol{U}}(\boldsymbol{u}).\)

  1. Apply the coordinate ascent algorithm to obtain the distribution for the optimal components.
  2. Write down an expression for the ELBO.
  3. Run the algorithm for the geyser data from MASS R package for \(K=2\) until convergence with \(\alpha=0.1, a=b=0.01.\) Repeat multiple times with different initializations and save the ELBO for each run.
  4. Repeat these steps for \(K=2, \ldots, 6\) and plot the ELBO as a function of \(K\). Comment on the optimal number of cluster components suggested by the approximation to the marginal likelihood.

Solution. 

#############################################################
## CAVI algorithm for K-components Gaussian mixture models
#############################################################
# Parameters are
# 1) weights w (probability of components)
# 2) cluster means mu
# 3) cluster variance sigma_sq
# 4) binary indicators of clusters "a" (data augmentation)
CAVI_gauss_mixt <- function(K = 2L, y,
                prior_mean_mu = rep(0, K),
                prior_var_mu = rep(1e8, K),
                prior_shape_var = rep(0.01, K),
                prior_rate_var = rep(0.01, K),
                prior_shape_weights = 0.01,
                maxiter = 1000L,
                tol = 1e-8
                ){
  stopifnot(K >= 1)
  K <- as.integer(K)
  n <- length(y)
  # ELBO normalizing constant (only depends on hyperparameters)
lcst <- 0.5*K*(1-n*log(2*pi)) +
  lgamma(K*prior_shape_weights) -
  K*lgamma(prior_shape_weights) -
  lgamma(n + K*prior_shape_weights)  +
  sum(prior_shape_var*log(prior_rate_var)) -
  sum(lgamma(prior_shape_var))
# Initialization
mu <- runif(K)*diff(range(y))
sigma_sq <- alpha <- rep(1, K)
A <- B <- rep(1, K) # K vector
ELBO <- numeric(maxiter)
nu <- matrix(NA, nrow = n, ncol = K)
# CAVI runs
for(b in seq_len(maxiter)){
  for(k in seq_len(K)){
    nu[, k] <- exp(digamma(alpha[k]) + 0.5*digamma(A[k]) - 0.5*log(B[k]) -
                   0.5*A[k]/B[k]*((y-mu[k])^2+ sigma_sq[k]))
  }
  omega <- nu/rowSums(nu) # Probability of components for each obs
  om <- colSums(omega) # sample size in each cluster
  sigma_sq <- 1/(1/prior_var_mu + A*om/B) # posterior variance of cluster
  mu <- sigma_sq*(prior_mean_mu/prior_var_mu + A/B*colSums(omega * y)) # posterior mean of cluster
  alpha <- prior_shape_weights + om
  A <- prior_shape_var + 0.5*om
  B <- prior_rate_var + 0.5*(colSums(omega*(outer(y, mu, FUN = "-")^2)) + om*sigma_sq)
  # Compute ELBO
  ELBO[b] <- lcst + sum(lgamma(A) - A*log(B) +
    lgamma(alpha) + 0.5*(log(sigma_sq) - log(prior_var_mu)) -
    0.5*((mu-prior_mean_mu)^2 + sigma_sq)/prior_var_mu) -
    sum(omega*log(omega+1e-80))
  if(b >=2){
    if((ELBO[b]-ELBO[b-1]) < tol){
      break
    }
  }
}
list(elbo = ELBO[1:b],
     mu_mean = mu,
     mu_var = sigma_sq,
     sigmasg_shape = A,
     sigmasg_rate = B,
     weights_alpha = alpha,
     probs = omega,
     mean_probs = alpha/sum(alpha),
     cluster_probs = colSums(omega)/sum(omega)
)
}
Code 
# Fit the model
data(geyser, package = "MASS")
mixt <- CAVI_gauss_mixt(K = 2, y = geyser$duration)
plot(mixt$elbo, 
     xlab = "number of iterations", 
     ylab = "evidence lower bound", 
     type = "b")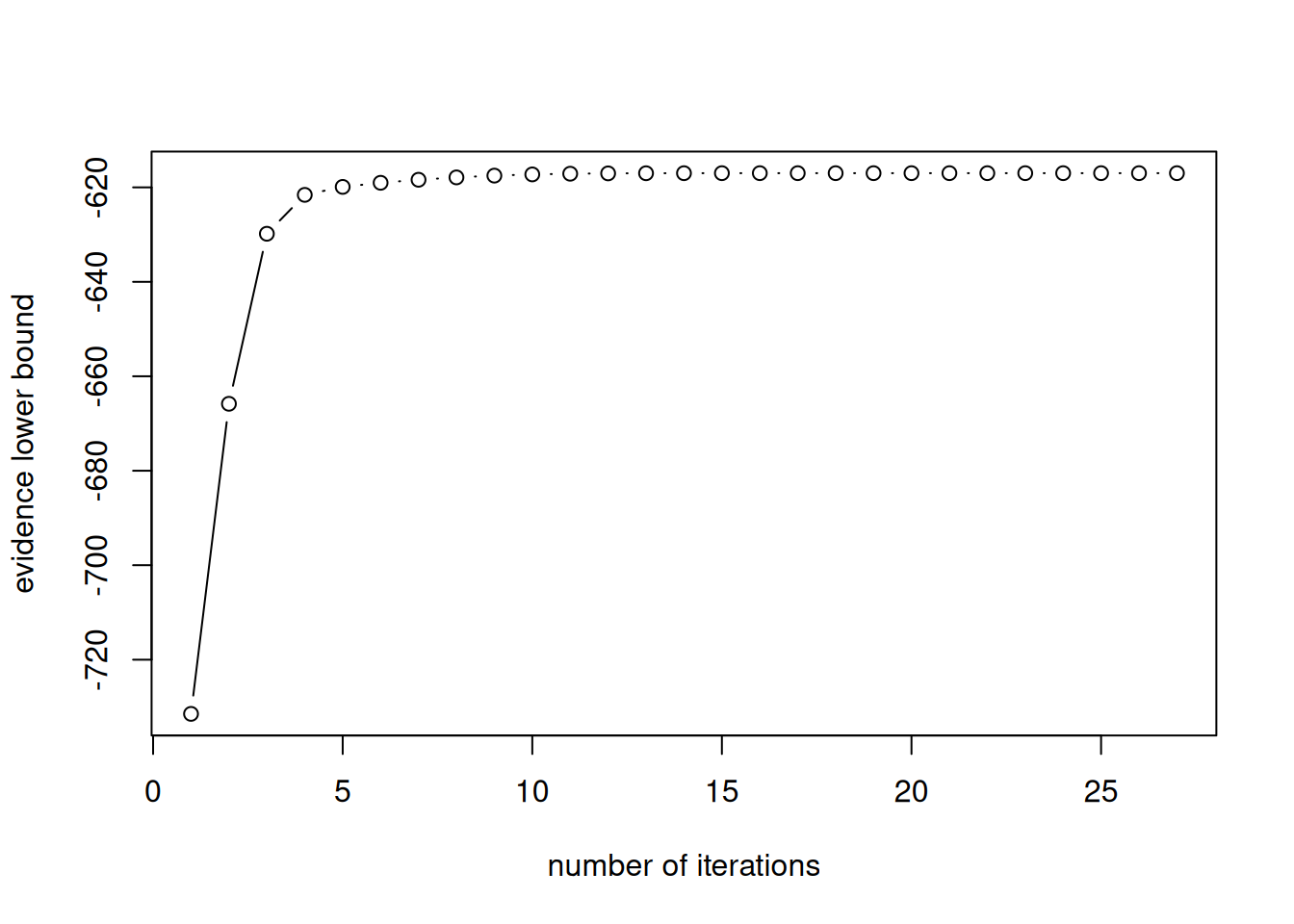

Code 
# Compute posterior mean of mean, variance and probability of each cluster
post_prob <- mixt$mean_probs
post_mean <- mixt$mu_mean
post_sd <- sqrt(mixt$sigmasg_rate/(mixt$sigmasg_shape-1))
# Plot the mixture density at posterior mean
curve(post_prob[1]*dnorm(x, mean = post_mean[1], sd = post_sd[1]) +
        post_prob[2]*dnorm(x, mean = post_mean[2], sd = post_sd[2]),
      from = 1,
      to = 6,
      n = 1001,
      xlab = "duration of geyser eruption (in minutes)",
      ylab = "density")
rug(geyser$duration)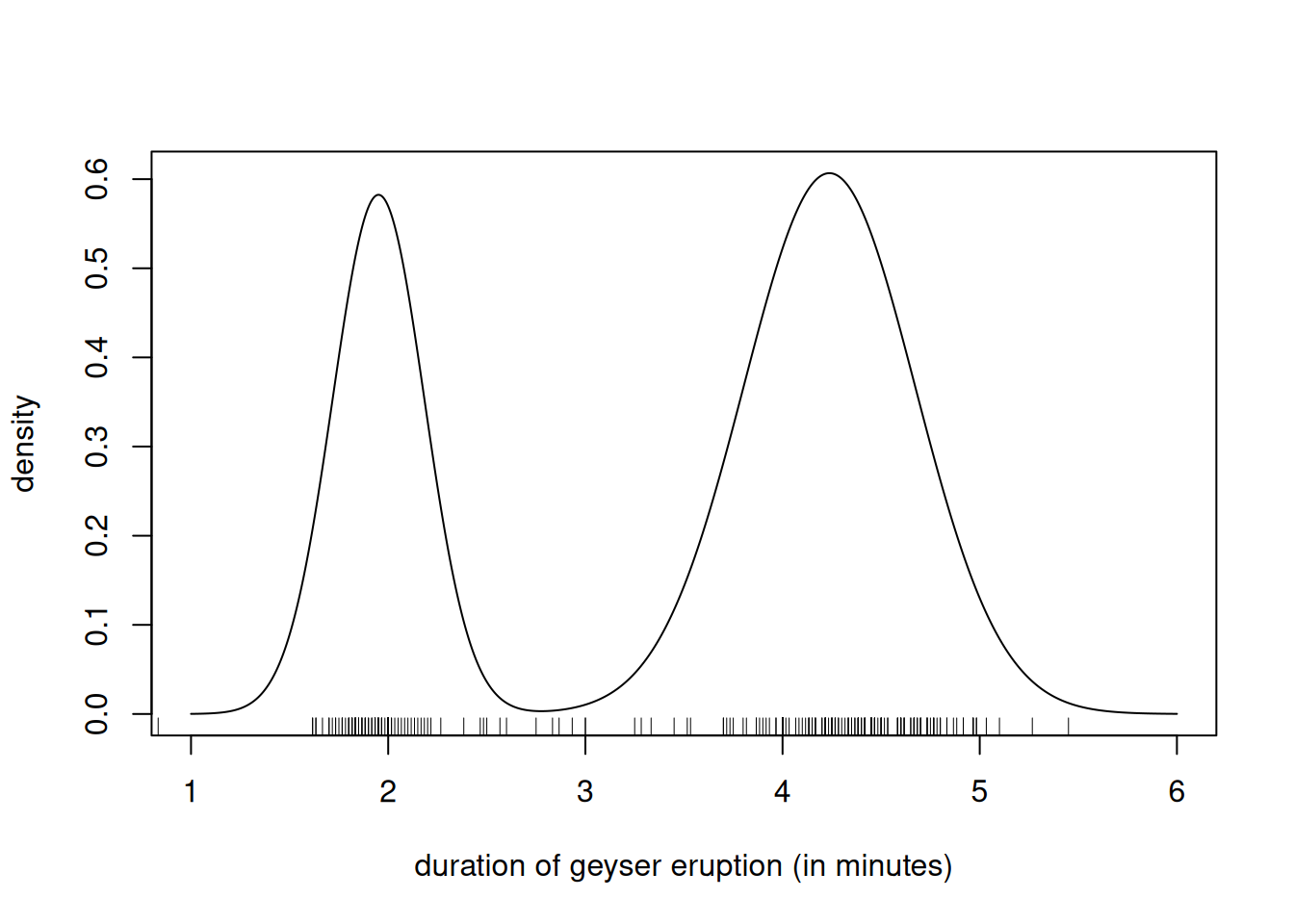

Footnotes

  1. Note that this is not a variational approximation!↩︎