7.2 Model selection invalidates P-values

Variable selection invalidates the usual Student and Fisher tests. To see this, we can generate a dataset \(\boldsymbol{y} = \boldsymbol{\varepsilon}\) and create an \(n \times p\) design matrix \(\mathbf{X}\) with random uncorrelated elements. We can assess by means of simulation the size distortion (the difference between the nominal level and the type I error) of a \(t\) test for the hypothesis \(\beta_j=0\) after performing forward selection.

We illustrate the computations using two models: one in which the variables in the design matrix, \(\mathbf{X}\), are strongly correlated and another with independent input using BIC and Mallow’s \(C_p\) as selection criterion. The size distortion is comparable.

## Uncorrelated variables, model selection using BIC

##                   size
## model                 0.1   0.05   0.01
##   Lowest BIC model 0.1696 0.1060 0.0344
##   Correct model    0.1056 0.0534 0.0094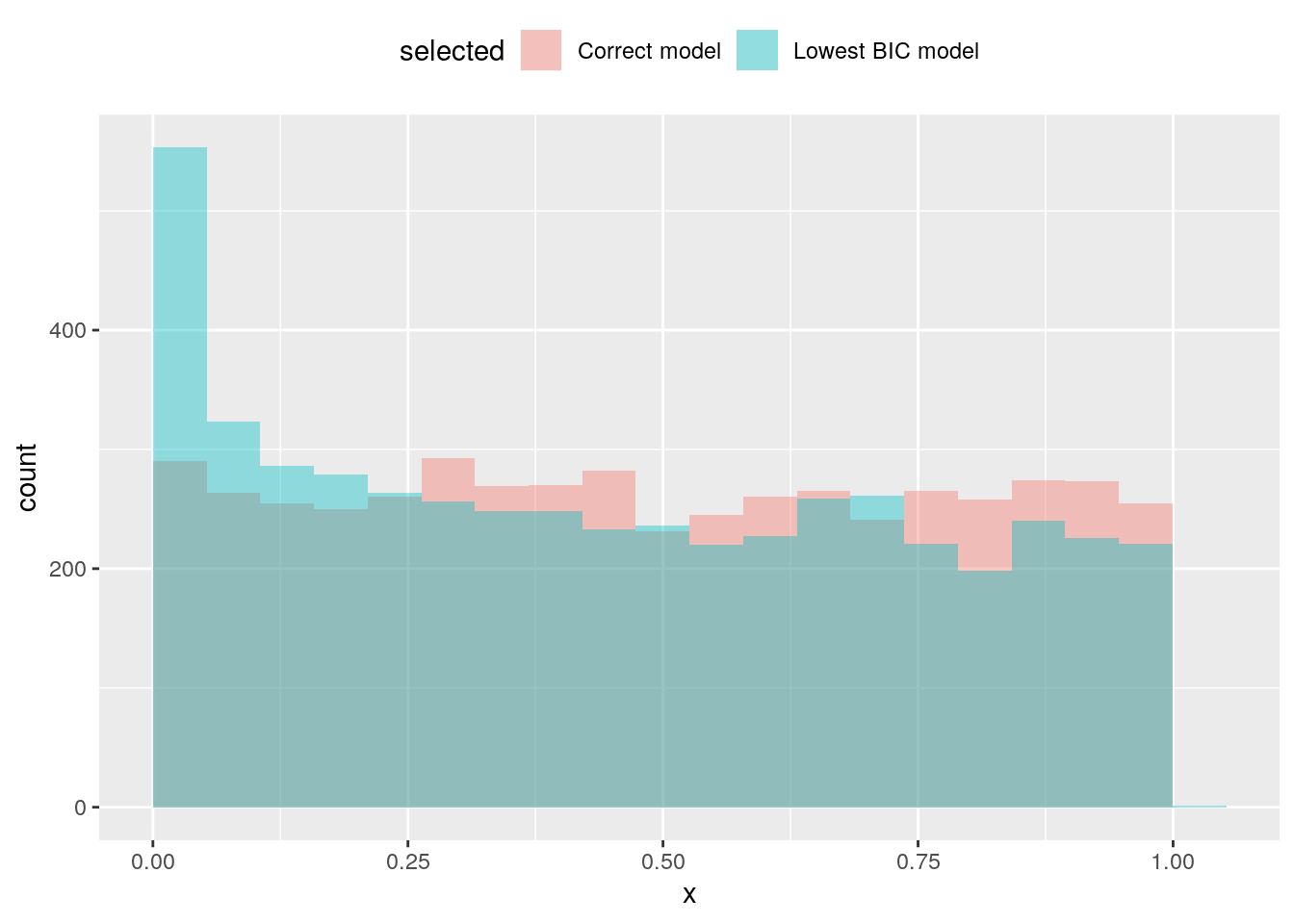

## Correlated variables, model selection using BIC

##                   size
## model                0.1   0.05   0.01
##   Lowest BIC model 0.190 0.1164 0.0350
##   Correct model    0.104 0.0516 0.0102

## Uncorrelated variables, model selection using Mallow's Cp

##                  size
## model                0.1   0.05   0.01
##   Lowest Cp model 0.1858 0.1092 0.0374
##   Correct model   0.1012 0.0504 0.0120

## Correlated variables, model selection using Mallow's Cp

##                  size
## model                0.1   0.05   0.01
##   Lowest Cp model 0.1872 0.1128 0.0356
##   Correct model   0.1026 0.0518 0.0086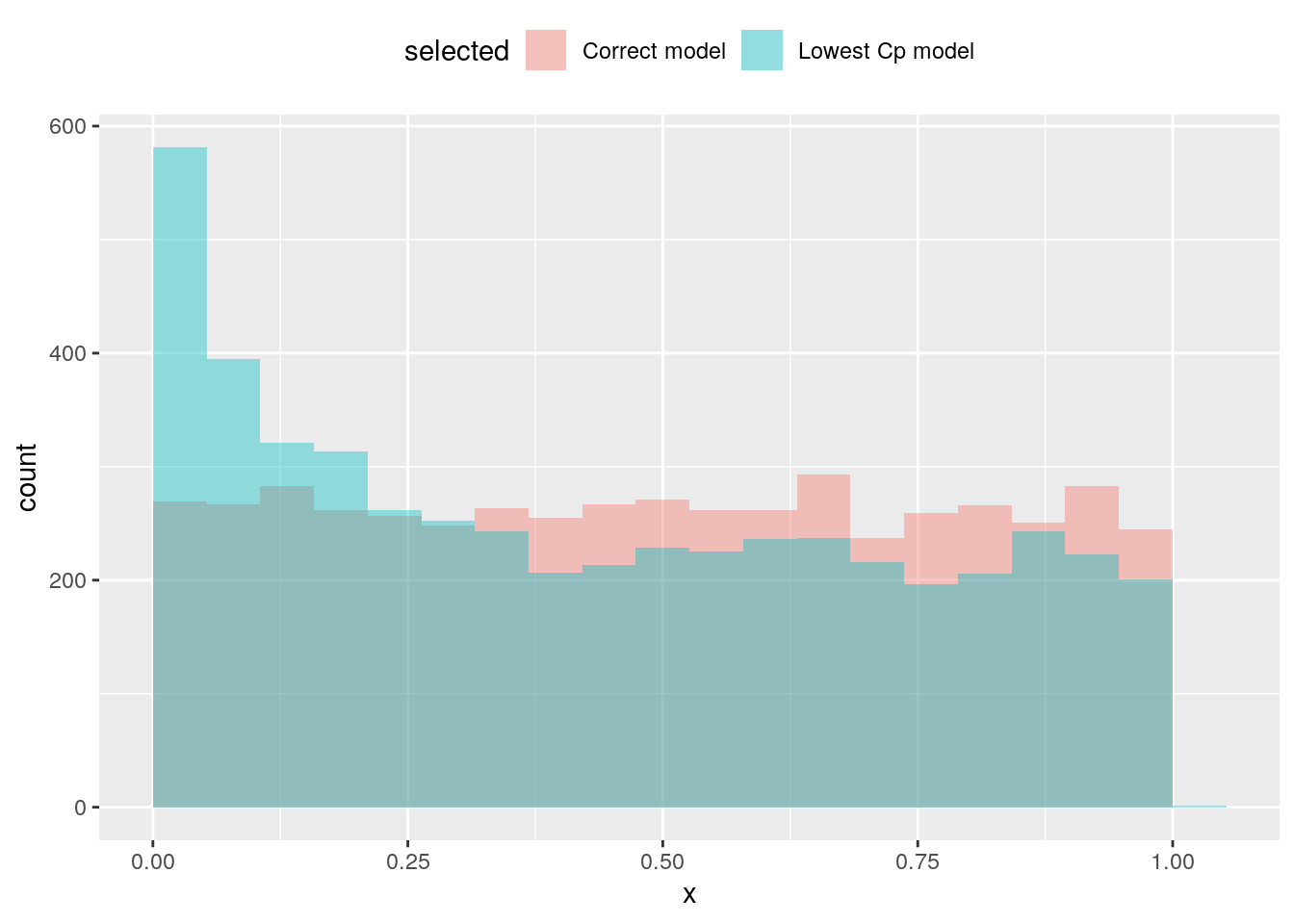

Adding superfluous variables does not induce bias, but inflates the standard errors (leading to larger \(P\)-values). We observe on the contrary here smaller \(P\)-values. Recall that the \(P\)-values should be uniformly distributed under the null hypothesis (and they seemingly are when the true null model is fitted).